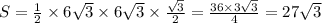Втреугольник abc вписана окружность с центром o. прямая bo вторично пересекает описанную около треугольника abс окружность

Question

Геометрия: Втреугольник abc вписана окружность с центром o. прямая bo вторично пересекает описанную около треугольника abс окружность в точке p. 1) докажите, что углы pco и pocравны. 2) найдите площадь треугольника apc, если радиус описанной окружности равен 6, а угол abc = 120 градусов.

antihype3 · Answer

Все обозначения на рисунке.

Углы ABO, CBO равны, т.к. BO - биссектриса, аналогично равны углы BCO и OCA; Дуги AP и PC равны => AP=PC => углы PAC и ACP равны. Угол ABP равен углу ACP, так как они опираются на одну дугу.

1) Выразим через x и y угол PCO: PCO=x+y; Теперь угол POC: POC=180-BOC; BOC=180-x-y => POC=180-(180-x-y)=x+y; Значит PCO=POC что и требовалось.

2) Из доказанного ранее, что не умаляет очевидности этого факта, AP=PC; Так как угол ABC = 120, то угол APC=60; Следовательно треугольник APC является равносторонним. Найдем AC по известной формуле: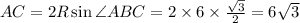 $AC=2R\sin \angle ABC=2\times 6\times \frac{\sqrt{3}}{2} =6\sqrt{3}$ ; Площадь треугольника APC: $S=\frac{1}{2}\times 6\sqrt{3}\times 6\sqrt{3} \times \frac{\sqrt{3}}{2}=\frac{36\times3\sqrt{3}}{4}=27\sqrt{3}$

Втреугольник abc вписана окружность с центром o. прямая bo вторично пересекает описанную около треуг

Популярные вопросы