Втрапеции авсd с основаниями аd и вс диагонали пересекаются в точке о.площадь треугольника вос равна 4, площадь треугольника аоd равна 9.найдите площадь трапеции.
Ответы
Треугольники 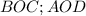 подобны
подобны
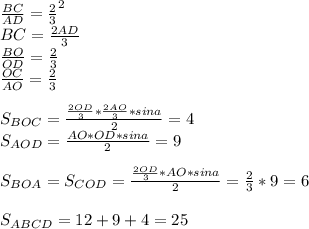
ПОКАЗАТЬ ОТВЕТЫ
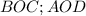 подобны
подобны 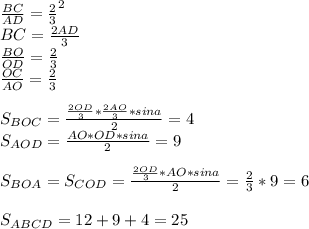
Другие вопросы по теме Геометрия
Популярные вопросы
- Найти частное решение y -4√2y +6y=0 , ...
2 - Мой chopp ер заставил его танцевать Мои купюры красные, будто я Blood...
2 - Порівняти створінь розвитку частин мозку жаби і риби?...
1 - 114. Измените глаголы вскобках так, чтобыОни сочетались с местоимениями....
1 - подъемный кран поднимает бетонную плиту весом 800 Н на высоту 10м за...
2 - Зробіть підсумок про особливості будови головного мозку...
3 - 74;296;1184...найти четвертый член геометрической прогрессии...
3 - В чем были ошибки правительства Калвина Кулиджа в экономике?...
3 - Определи вид информации по форме представления.Установи соответствие...
2 - Задание №1 Заполните таблицу, сравните пути объединения Италии и Германии...
2