Вспомнил, геометрия. 5/5
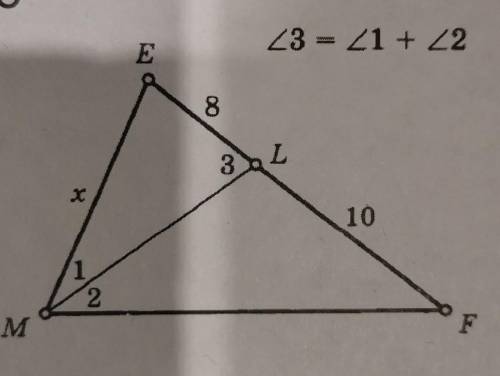
Найдите x​

Для нахождения значения x в этой задаче, мы должны использовать свойства и принципы геометрии. Данная задача связана с прямыми и треугольниками.

Нам дана схема с двумя пересекающимися прямыми AB и CD. Нам нужно найти значение x.

Давайте рассмотрим эту ситуацию подробнее:
1. Заметим, что угол DAB и угол ABC являются вертикальными углами, поэтому они равны друг другу. Таким образом, мера угла DAB равна 80 градусам.
2. Заметим, что угол ACD и угол DCB являются вертикальными углами, поэтому они равны друг другу. Таким образом, мера угла ACD равна 70 градусам.
3. Заметим, что угол BCD и угол DCB являются смежными углами, поэтому их сумма равна 180 градусам. Таким образом, мера угла BCD равна 180 - 70 = 110 градусам.

Теперь, когда мы знаем меру угла BCD, мы можем рассмотреть треугольник BCD:
4. В треугольнике BCD сумма мер углов равна 180 градусам. Мы уже знаем, что мера угла BCD равна 110 градусам. Таким образом, мы можем записать уравнение: 110 + мера угла BDC + мера угла CBD = 180.
5. Заметим, что угол DBC и угол BDC являются смежными углами, поэтому их сумма равна 180 градусам. Таким образом, мы можем записать уравнение: 110 + мера угла DBC + мера угла BDC = 180.
6. Поскольку угол DBC и угол BDC имеют одинаковые меры (они являются вертикальными углами), мы можем записать уравнение: 110 + мера угла DBC + мера угла DBC = 180.
7. Упрощая уравнение, получаем: 110 + 2 * мера угла DBC = 180.
8. Теперь нужно решить это уравнение, выражая меру угла DBC.
- Вычитаем 110 из обеих сторон уравнения: 110 + 2 * мера угла DBC - 110 = 180 - 110.
- Упрощаем: 2 * мера угла DBC = 70.
- Делим обе стороны на 2: (2 * мера угла DBC) / 2 = 70 / 2.
- Упрощаем: мера угла DBC = 35 градусов.

Теперь, когда мы знаем меру угла DBC, мы можем рассмотреть треугольник ABD:
9. В треугольнике ABD сумма мер углов равна 180 градусам. Мы уже знаем, что мера угла DAB равна 80 градусам, а мера угла DBC равна 35 градусов. Таким образом, мы можем записать уравнение: 80 + 35 + мера угла DDA = 180.
10. Суммируем известные значения: 80 + 35 + мера угла DDA = 180.
11. Упрощаем: 115 + мера угла DDA = 180.
12. Вычитаем 115 из обеих сторон уравнения: 115 + мера угла DDA - 115 = 180 - 115.
13. Упрощаем: мера угла DDA = 65 градусов.

Таким образом, мы вычислили все значения углов в данной схеме. Значение x представляет собой меру угла DDA, которое составляет 65 градусов.