Вспомнил, геометрия. 2/5
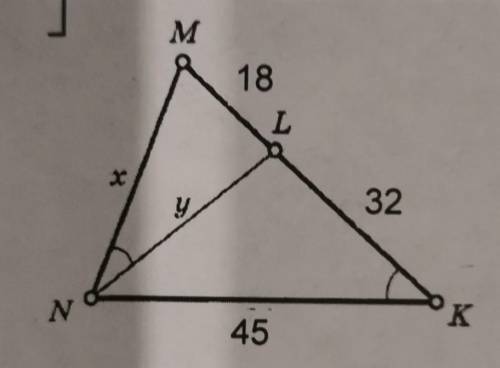
Найдите x и y​

треугольники NML и NMK подобны по двум углам (угол N = угол K по условию, угол M - общий), тогда

18/х = х/50

х × х = 18 × 50

х² = 900

х = 30

также

у/45 = х/50

50у = 45 × 30

у = 27

Для решения данной задачи, мы можем воспользоваться знаниями о пропорциях.

Изображение представляет собой параллелограмм ABCD.

У нас есть две параллельные стороны, AB и CD, которые имеют одинаковую длину. Примем длину этих сторон за y.

Также у нас есть две секущие, AD и BC, которые пересекаются в точке O. Примем отрезок AO за x.

Заметим, что треугольники AEO и CBO являются подобными, так как они имеют два равных угла: угол AEO равен углу CBO (вертикальные углы), а также угол AOE равен углу COB (опять же, вертикальные углы).

Используя это свойство подобных треугольников, мы можем записать пропорцию отношения длин сторон треугольников AEO и CBO:

AE/OB = EO/OC

Знаем, что длина AE равна половине длины AB, то есть AE = AB/2. В нашем случае AB = y, поэтому AE = y/2.

Длина OB равна разности длин стороны AB и отрезка AO, то есть OB = AB - AO. В нашем случае AB = y и AO = x, поэтому OB = y - x.

Теперь мы можем записать пропорцию:

(y/2)/(y - x) = (EO)/(OC)

Заметим, что длина EO равна разности длин AB и AD, то есть EO = AB - AD. В нашем случае AB = y и AD = x, поэтому EO = y - x.

Длина OC равна отрезку OB, то есть OC = OB = y - x.

Подставим в пропорцию значения EO и OC:

(y/2)/(y - x) = (y - x)/(y - x)

Теперь мы можем упростить пропорцию:

(y/2) = (y - x)

Раскроем скобки:

y/2 = y - x

Умножим обе части уравнения на 2, чтобы избавиться от дроби:

2*(y/2) = 2*(y - x)

y = 2y - 2x

Перенесем все элементы с x на одну сторону уравнения:

2x = y

Теперь разделим обе части уравнения на 2:

x = y/2

Таким образом, мы получаем, что x равно половине значения y.

Ответ: x = y/2.