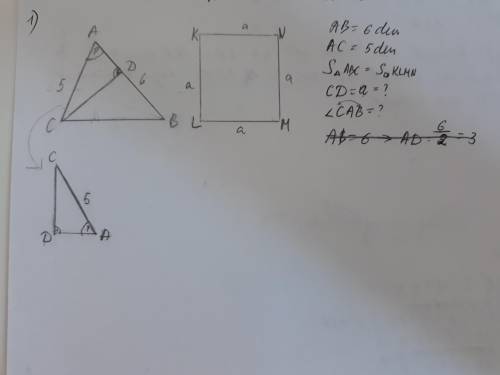
Все стороны остроугольного треугольника ABС равны АВ=6 дм и АС=5 дм. Площадь треугольника АВС равна площади квадрата, сторона которого равна высоте СD проведённое от вершины С. Найдите угол ВАС
лиана252
1
29.05.2021 16:00
1
Другие вопросы по теме Геометрия
Ксения26941479
16.08.2022 05:20
dkogotyzeva
18.08.2022 10:09
borkunovanasta
06.12.2020 21:15
aleXxxx03
06.12.2020 21:14
daniilznanija0
06.12.2020 21:13
235www
14.05.2020 23:04
hitman19102003
14.05.2020 23:05
elnur22
14.05.2020 23:06
marisshechka1
14.05.2020 23:06
Популярные вопросы
- Составить комплекс упражнений с фитболом на урок по теме Волейбол...
3 - Тікбұрыштың көршілес төбелерін , көршілес кабыргаларын атау...
3 - Посмотрите на картинки выше. На них изображены герои разных, может быть, даже...
3 - Дана блок-схема. Какое значение будет иметь z на выходе, если x=38?...
3 - (2а+а)+(5-а)(5+а) при х=-3/4...
2 - 1 в XX веке не был изобретён:А) компьютер;Б) телевизор;В) корабль.2. В XX веке...
3 - Что такое гормоны и каковы их свойства?...
3 - Match the words. Then use five of them to complete the sentences....
2 - Из приведенных утверждений выберите те, которые относятся к характеристике химического...
3 - Задание №1. Заполни схему, используя предложенную ниже информацию, соблюдая...
3
SΔABC =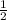
CD×AB
S KLMN = a²
3a = a²
3a - a² =0
a(3 - a) = 0
a₁ = 0, или 3 - а = 0; а₂ = 3
a = 0 - не подходит
а = 3
По теореме синусов:
5sin∠CAD = 3
sin∠CAD = 0,6
∠CAD = 37°