1. Геометрия
  2. Вравнобокой трапеции перпендикулярно

Вравнобокой трапеции перпендикулярно к боковой стороне проведена диагональ образовывая угол 30 градусов с основанием , найдите площадь трапеции . трапеция вписана в оружность и радиус равен r

petrenko20002 petrenko20002    2   19.07.2019 15:23    3

Ответы
vanyaburundukov vanyaburundukov  19.08.2020 13:48

Поскольку В и С видны под одним и тем же углом, то точки A,B,C,D лежат на окружности с диаметром AD = 2R. Из прямоугольного треугольника ACD: против угла 30° катет в два раза меньше гипотенузы, т.е. CD = AD/2 = R, ∠D = 90° - 30° = 60°.

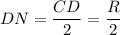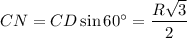
Из прямоугольного треугольника CND: DN=\dfrac{CD}{2}=\dfrac{R}{2} и CN=CD\sin 60^\circ=\dfrac{R\sqrt{3}}{2}

\dfrac{AD-BC}{2}=ND~~\Rightarrow~~~ BC=AD-2ND=2R-2\cdot\dfrac{R}{2}=R

Площадь трапеции: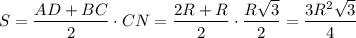 S=\dfrac{AD+BC}{2}\cdot CN=\dfrac{2R+R}{2}\cdot\dfrac{R\sqrt{3}}{2}=\dfrac{3R^2\sqrt{3}}{4} кв. ед.


Вравнобокой трапеции перпендикулярно к боковой стороне проведена диагональ образовывая угол 30 граду
ПОКАЗАТЬ ОТВЕТЫ
KaraKiller KaraKiller  19.08.2020 13:48

Решение на фото//////////


Вравнобокой трапеции перпендикулярно к боковой стороне проведена диагональ образовывая угол 30 граду
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
ИльяКорецкий ИльяКорецкий  09.05.2019 11:02
Визначте кількість сторін многокутника, у якого кожний зовнішній кут дорівнює 40°.визначте кількість сторін многокутника, у якого кожний зовнішній кут дорівнює 40°....
Tanya20042017 Tanya20042017  09.05.2019 11:02
Dabc – тетраэдр, m – точка пересечения медиан треугольника авс, точка к лежит на dc так, что dk : kc = 3 : 2 разложите вектор mk по векторам ba=a , bc =c , bd =d...
Cesar123213 Cesar123213  09.05.2019 11:04
Вокружности с центром o проведена хорда ab, равная радиусу окружности. найдите углы треугольника aob. ​...
leksios leksios  09.05.2019 11:10
Хорда ab стягивает дугу, равную 99 , а хорда ac - дугу в 57. найдите угол bac должно быть 2 варианта ответа...
snezhkabo00 snezhkabo00  09.05.2019 11:11
Многокутник, який є 17-ти кутником, має діагоналей....
emuratov606Erali emuratov606Erali  09.05.2019 09:23
Точка - o центер , кола зображеного на рискнку . знайдіть градусну міру кута abc ....
Kenny22332 Kenny22332  14.07.2019 00:20
Впрямоугольнике авск диагонали пересекаются в точке о.угол авк больше угла свк на 20 градусов.найдите углы треугольника аок...
Настя2017465 Настя2017465  14.07.2019 00:20
Хорда ab делит дугу окружности с центром o на две части,отношение которых равно 6: 9.найдите величину центрального угла aob,если дуга ab имеет меньшую градусную меру...
Катрина228Беккер Катрина228Беккер  14.07.2019 00:20
Нужна в прямоугольном треугольнике авс угол в равен 15 градусам. из вершины прямого угла с проведена высота сн и медиана см. найдите отношения сн : ав и мн : вс....
denus16 denus16  08.09.2021 20:04
12. Найти радиус окружности, описанной около прямоугольного треугольника с катетами 8 см и 15 см. A) 7,5 см; B) 17 см; C) 8,5 см; D) 9 см....

Популярные вопросы