Вравнобокой трапеции основания равны 4см и 10см, а угол между боковой стороной и большим основанием равен 30 градусов. найти: 1) среднюю линию; 2) высоту; 3) боковую сторону трапеции. 60 ! , !

1. 7

2.

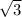
3.

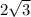
Объяснение:

1. m(средняя линия)= =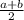

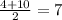
2.  Обозначим за х- высоту.

Тогда 2х-боковая сторона трапеции.

(Рассматривая треугольник, где высота- катет прямоугольного треугольника, она лежит против угла в 30 градусов, значит будет равна половине гипотенузы, или же боковой стороны).

Другой катет этого треугольника, будет равен 3.

(т.к. если провести вторую высоту в трапеции, то получится прямоугольник и 2 треугольника, т.к. это равнобедренная трапеция, то эти треугольники будут равны => 10-4= 6,  6:2=3)

По т. Пифагора, найдем высоту и боковую сторону:

3=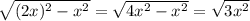

-высота.

2*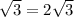-боковая сторона.

Вроде должно быть так, если заметите ошибку, то скажите.