Вравнобедренную трапецию с длинами оснований 4 и 16 см вписана окружность. чему равен ее радиус (см)?

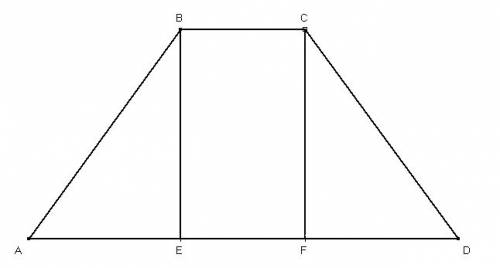
Пусть в трапецию ABCD, AD=16, BC=4 вписана окружность. Радиус окружности, вписанной в трапецию, равен половине высоты трапеции. Если в трапецию можно вписать окружность, значит, суммы её противоположных сторон равны, то есть, сумма 2 боковых сторон равна сумме оснований - 16+4=20, а так как боковые стороны равны, то каждая из них равна 20/2=10. Проведём высоты BE и CF. Четырехугольник BCFE является прямоугольником, так как все его углы прямые. Тогда EF=BC=4. Треугольники ABE и CDF равны по катету и гипотенузе (AB=CD; BE=CF). Тогда AE=DF=(AD-EF)/2=(16-4)/2=6. В прямоугольном треугольнике ABE гипотенуза AB равна 10, а катет AE равен 6. Тогда катет BE по теореме Пифагора равен √10²-6²=√100-36=√64=8. Отрезок BE является высотой трапеции и равен 8, тогда радиус вписанной окружности вдвое меньше и равен 8/2=4 см.