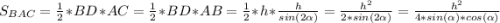Вравнобедренном треугольнике высота, проведённая к боковой стороне, равна
h и образует с основанием угол α. найти площадь треугольника.
Другие вопросы по теме Геометрия
Популярные вопросы
- Ленту длинной 14м разрезали на 4 равные части какова длинна одной...
2 - Решите )это сольфеджио 3 класс...
1 - Выражение 10*2 в степени n 2 в степени n+1- 2 в степени n-1...
2 - Нужна по lazarus. есть два combobox-а, в каждом из них список...
3 - Разберите слова по составу [прист. корень суф.] бледнела,краснеешь,вооружает,разоружаешь,заболели,поправляешься,научишься,разучилась....
2 - Магнитное поле возникает вокруг: 1)движущегося атома2)покоящегося...
2 - Вкакой стране побывала алиса во время своих приключений?...
1 - Заполните таблицу: «реформы 1867 – 1868 годов в казахстане»...
1 - Найдите координаты вектора pk, если p(-3; 4),k(-9; 2) . а) (-6:...
2 - Для того, чтобы наполнить бак на даче, павлу андреевичу нужно...
3
Объяснение:
BD = h, ∠DBC=α , AB = AC = x, BD - высота, S=?
1) BD - высота => BD⊥AC => ∠BDC = ∠BDA = 90°
2) В ΔBDC ∠BDC=90° => ∠BCD = 90° - α
3) В ΔBAC ∠BAC = 180° - ∠ABC - ∠BCA = 180° - 2∠BCA = 180° - 2(90° - α) = 180° - 180° + 2α = 2α
4) В ΔBDA ∠BDA=90° =>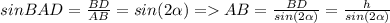
5)