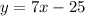Вравнобедренном треугольнике авс заданы вершины с(4; 3), уравнение 2х – у – 5 = 0 основания ас и уравнение х – у = 0 боковой стороны (ав). написать уравнение стороны вс.
Другие вопросы по теме Геометрия
Популярные вопросы
- Чем отличается считалкой и небылицей?...
3 - Решите уравнение 4 (целых) 7/12 - у = 2,5...
1 - Вкаких клетках больше всего аппарата гольджи - в мышечных или в клетках...
2 - На базу 60 т капусты сколько капусты осталось на базе если в магазины отправили...
1 - Синоним к словам проворный коростель...
3 - Решить по 2 класс 9 си заданные 1 лопата? 2 завод? 3 работа?...
2 - Укажите характерные особенности внешнего строения: а)древнейших б)древних...
3 - 4. в октябре 1994 года наблюдалось интенсивное извержение вулкана ключевская...
2 - Не могу найти закономерность 5 10 17 22 какая следуишая цифра?...
2 - Копошился это словарное слово? если нет подберите проверочное слово...
2
Будем искать координаты точки исходя из равенства векторов и принадлежности прямой
исходя из равенства векторов и принадлежности прямой 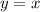
Пусть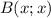 , т.к. точка лежит на прямой
, т.к. точка лежит на прямой 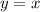
Отсюда получаем, что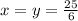
Общее уравнение прямой, проходящей через точки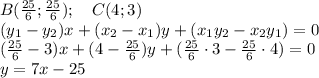
ответ: