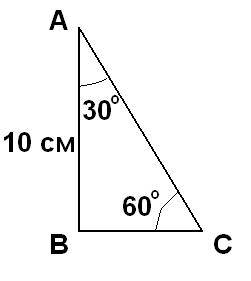
Впрямоугольном треугольнике один из катетов равен 10, а угол лежащий напротив него равен 60 градусам. найдите площадь треугольника.
Ответы
Так как треугольник прямоугольный, то <A (см.рисунок во вложении) = 90 - <C = 90 – 60 = 30 градусов. Как известно, в прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Таким образом если этот катет, т.е. катет ВС обозначить Х, то гипотенуза т.е. сторона АС =2Х. По теореме Пифагора (АС)^2 = (AB)^2 + (BC)^2. Подставив в это уравнение принятые и известный отрезки имеем (2Х)² = 10² + X², или 4Х²= 10²+ X² или 3Х²= 100. Отсюда Х²= 100/3 и малый катет, т.е. Х = √(100\3) = 10/√3. Площадь прямоугольного треугольника равна половине произведения его катетов. Т.е. S = (АВ*ВС)/2 = 10*10/2√3 = 50/√3
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Стену длиной 6 метров и высотой 3 метра хотят выложить кафелем. одна плитка имнэеет...
3 - Разложите на множители: 1)3(t + 2) - t(t + 2) = (t + 2)(3 - t) 2)ab(b-3)+a^2(b-3)...
1 - Какое из чисел является рациональным? √0,144 √1440 √144 √0,064...
2 - (под сенью) замените общеупотребительным...
2 - Расскажите про правление лжедмитрия 1(кратко)...
1 - Выпишите 2 словосочетания, содержащие в себе 1) прилагательное 2) причастия 3)...
1 - Изложение храбрость. на тропепе сидел молодой вообушек.вдруг собака уменьшела...
3 - Слово из согласных с,к,л, и любых согласных и чтоб с, к, л использовались в каждом...
1 - Периметр прямоугольника 312 см. найдите его площу, если одна сторона прямоугольника...
3 - При каком значении х значения выражений 1,2х+7и 2х+3 равны ?...
1