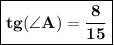Впрямоугольном треугольнике abk гипотенуза ab равна 17, катет ak равен 15. найдите тангенс угла а ( 8 класс )
Другие вопросы по теме Геометрия
Популярные вопросы
- Реши с уравнения по озеру плавало 34 лебедя . после того как несколько...
2 - Вслове петушок звук п твердый или мягкий...
2 - Зелений -- зелень. який б словотворення та чому він?...
2 - Дополни предложения: а) устройство ввода данных- б) устройство хранения...
1 - Моя лучшая подруга сочинение с планым можно по быстрее заранее...
1 - Прочитай рассказ и выбери верные утверждения: говорят, хитрей лисицы...
1 - Вчем заключаются особенности драматургии гоголя? !...
1 - Бородин князь игорь краткое содержание...
2 - Написать волшебную сказку примерно на 20/25/15предложений...
1 - Один из углов треугольника равна 150 градусов и противолежащий сторона...
2
Дано: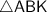 - прямоугольный,
- прямоугольный,  - гипотенуза,
- гипотенуза, 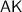 - катет.
- катет.
Найти: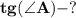
------------------------------------------------------------------------------------------
В прямоугольном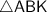 -
- 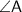 острый.
острый.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Найдём катет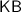 по теореме Пифагора:
по теореме Пифагора:
Зная величину обоих катетов, найдём тангенс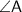 :
:
ответ: