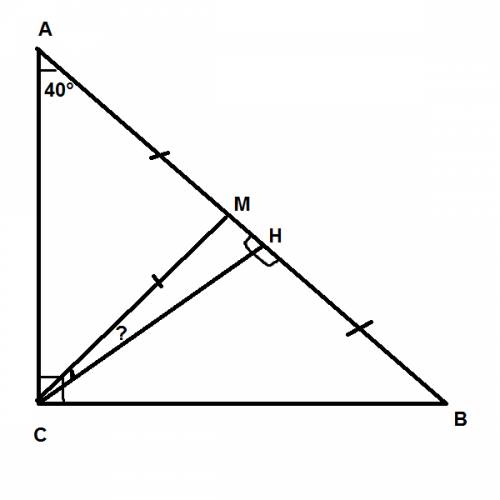
Впрямоугольном треугольнике abc угол c равен 90,угол a - 40.найдите угол между медианой и высотой,проведенными из вершины c.

Пусть CH - высота треугольника ABC, а CM - его медиана. Угол B = 90° - 50° = 40°. Следовательно, можем найти угол BCH в треугольнике CHB, Так как CH - высота, то треугольник BCH - прямоугольный. Значит, угол BCH = 90° - 50° = 40°. По свойству медианы прямоугольного треугольника CM = 0,5 AB = AM = MB (так как медиана CM делит гипотенузу пополам). Знаичт, треугольник BCM - равнобедренный. У равнобедренного треугольника углы при основании равны, значит угол MCB = B = 50°. Рассмотрим треугольник MCH. Угол MHC = 90°, так CH - высота. Сумма двух острых углов прямоугольного треугольника 90°, значит угол MCH = 90° - 80° = 10°.