Впрямом параллелепипеде abcda1b1c1d1 ab=1,bc=7(корень)3,угол abc=150. через диагональ ас и вершину в1 проведена плоскость,составляющая с плоскостью основания угол 60. найдите площадь боковой поверхности параллелепипида.
Другие вопросы по теме Геометрия
Популярные вопросы
- Ех.4р.101(составить квиз о российском празднике пошалуйста...
2 - Рассчитать по алгоритму энергию связи урана 242 и алюминия 227...
1 - Які реформи провела Єлизавета Петрівна?...
1 - ТАБЛИЦА. СОСЛОВИЯ В РОССИИ 17 ВЕКА...
1 - нужна Химия, Подгруппа кислорода...
2 - 5 в квадрате? Сколько будет 5 в квадрате...
2 - Определи площадь треугольника , если = 17 см, ∡=40°, ∡=75°....
3 - Напиши один диалог по маршрутам (используя карту)на фотке• The hospital to the...
2 - Решите уравнения, показывая, как переносите слагаемые 0,3x+5,1=0,7x-4,9 3x-12=10,5x+3...
1 - They ... a real tiger in the zoo a) seed b) has seen c) saw d) have seen...
2
Объяснение:
Площадь боковой поверхности прямого параллелепипеда:
S = Росн · ВВ₁
Росн = 2(AB + BC) = 2(1 + 7√3)
Проведем ВН⊥АС. ВН - проекция В₁Н на плоскость основания, значит
В₁Н⊥АС по теореме о трех перпендикулярах, ⇒
∠В₁НВ = 60° - линейный угол двугранного угла между плоскостями (В₁АС) и основанием.
ΔАВС: по теореме косинусов:
АС² = AB² + BC² - 2·AB·BC·cos∠B
AC² = 1 + 147 + 2 · 7√3 · √3/2 = 148 + 21 = 169
AC = 13
Sabc = 1/2 AB · BC · sin∠B = 1/2 · 7√3 · 1/2 =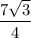
Sabc = 1/2 AC · BH
ΔBB₁H:
tg∠B₁HB = BB₁ / BH
BB₁ = BH · tg60°