Вправильной пирамиде sabc r- середина ребра bc, s-вершина. известно что ab=8, а площадь боковой поверхности равна 252. найдите длину отрезка sr

Question

Геометрия: Вправильной пирамиде sabc r- середина ребра bc, s-вершина. известно что ab=8, а площадь боковой поверхности равна 252. найдите длину отрезка sr

Bazzaevat · Answer

SR - апофема пирамиды. Площадь боковой поверхности состоит из суммы площадей 3-х равных треугольников, которые являются боковыми гранями пирамиды. То есть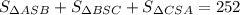 $S_{\Delta ASB}+S_{\Delta BSC}+S_{\Delta CSA}=252$ . В данном случае речь идет о треугольнике BSC. так как площади треугольников равны, то можно записать в следующем виде 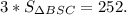$3*S_{\Delta BSC}=252.$ Делим обе части на 3. 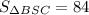$S_{\Delta BSC}=84$ . Так как треугольник BSR - равнобедренный (из того, что пирамида -правильная), то его площадь равна произведению половины основания BC на высоту SR. Так как пирамида правильная, то AB=BC.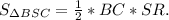 $S_{\Delta BSC}=\frac{1}{2}*BC*SR.$