Вправильной четырехугольной пирамиде боковое ребро и высота образует угол 30°. найдите площадь основания пирамиды, если высота равна 5 см.

 Обозначим пирамиду SABCD,  В правильной четырехугольной пирамиде основание – квадрат, боковые ребра равны,  вершина проецируется в центр основания, т.е. в точку пересечения его диагоналей.   Площадь квадрата по одной из формул равна половине произведения его диагоналей. S=d²/2.

   Ребро и высота пирамиды образуют угол ASO=30°. Высота перпендикулярна основанию, треугольник AOS, образованный ребром SA, высотой SO и половиной диагонали АО – прямоугольный. АО=SO•tg30° ⇒  0,5d=5•1/√3,  d=10/√3, S=0,5•(10/√3)²=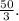   ед. площади.