1. Геометрия
  2. Впараллерограмме одна из

Впараллерограмме одна из диагоналей ,равная 18 см ,образует со сторонами углы 20 и 40 градусов .найдите стороны параллелограмма.

yubloh yubloh    2   05.10.2019 06:20    19

Ответы
KittyKittyk KittyKittyk  09.10.2020 21:09

AC = 18 см, ∠CAD = 20°, ∠BAC = 40°

Т.к. AB ║ CD, то ∠ACD = ∠BAC = 40° (как накрест лежащие)

Сумма углов ΔACD равна 180° ⇒ ∠ADC = 180° - ∠ACD - ∠CAD = 180° - 20° - 40° = 120°

По теореме синусов для ΔACD:

\frac{AD}{\sin{\widehat{ACD}}}=\frac{CD}{\sin{\widehat{CAD}}}=\frac{AC}{\sin{\widehat{ADC}}}\longrightarrow\\AD=\frac{AC*\sin{\widehat{ACD}}}{\sin{\widehat{ADC}}}=\frac{18*\sin{40}}{\sin{120}}=\frac{36*\sin{40}}{\sqrt{3}}=12\sqrt{3}*sin(40)\\CD=\frac{AC*\sin{\widehat{CAD}}}{\sin{\widehat{ADC}}}=\frac{18*\sin{20}}{\sin{120}}=\frac{36*\sin{20}}{\sqrt{3}}=12\sqrt{3}*sin(20)

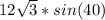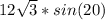ответ: Стороны параллелограмма равны: 12\sqrt{3}*sin(40) см и 12\sqrt{3}*sin(20) см


Впараллерограмме одна из диагоналей ,равная 18 см ,образует со сторонами углы 20 и 40 градусов .найд
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
АйкоУесМ АйкоУесМ  20.04.2020 16:22
Какие из векторов имеют прямой угол?...
redridinghood1 redridinghood1  20.04.2020 16:21
Периметр параллелограмма ABD равен 9 см, а периметр треугольника ABD равен 6,5 см. Рассчитатй BD...
Anna69666 Anna69666  20.04.2020 16:20
Определи скалярное произведение данных векторов, если длина ребра куба равна 15 ед. изм....
MariaWoLF2006 MariaWoLF2006  20.04.2020 16:20
В прямоугольном треугольнике проведена высота из верши-ны прямого угла. Докажите, что данный треугольник и дваобразовавшихся треугольника имеют соответственно равныеуглы...
angel20062006 angel20062006  22.05.2021 10:13
В треугольнике ABC плюс б равно BC MN параллельна AB и MN равно 16 см Найдите длину CD в сантиметрах​...
kotuk333 kotuk333  22.05.2021 10:12
Даны векторы а(2: -3) и b(-2:-3) найдите координаты вектора c=-3a-2b​...
MichiChi MichiChi  22.05.2021 10:06
Радиус окружности описаной около правильного треугольника равен 4√3 см....
Dashocheg43 Dashocheg43  22.05.2021 10:06
через вершину A прямокутника ABCD проведено пряму AL перпендикулярну до його площини . LB=3см LC=4,8см LD=4см знайдіть 1)AL 2)площину надо ​...
аня343213 аня343213  22.05.2021 10:06
Знайдить перимерт паралеограама, стороны якого доривнюють 5 см и 8см 2. Один з кутив ромба доривнюе 150 градусив. Знайдить инши кути ромба. 3. Знайдить площу трикутника одна зи сторин...
svetlanakorneev svetlanakorneev  22.05.2021 10:01
Вписанный угол на 27° меньше центрального угла, опирающегося на ту же дугу окружности. Чему равен вписанный угол?​...

Популярные вопросы