1. Геометрия
  2. Впараллелограмме стороны

Впараллелограмме стороны равны 8 и
7 \sqrt{3}
см, острый угол равен 30˚. найдите диагонали и площадь параллелограмма.​

VladeslavPavlo VladeslavPavlo    2   26.08.2019 12:10    1

Ответы
ektgdb ektgdb  05.10.2020 20:55

Тупой угол параллелограмма равен β = 180° - 30° = 150°

Пусть a,b - стороны параллелограмма,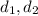 d_1,d_2 - его диагонали.

Площадь параллелограмма: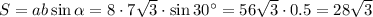 S=ab\sin\alpha =8\cdot 7\sqrt{3}\cdot \sin30^\circ=56\sqrt{3}\cdot 0.5=28\sqrt{3} см²

По теореме косинусов:

d_1^2=a^2+b^2-2ab\cos \alpha\\ d_1^2=8^2+(7\sqrt{3})^2-2\cdot 8\cdot 7\sqrt{3}\cdot \frac{\sqrt{3}}{2}\\ d_1^2=64+147-168\\ d_1^2=43\\ d_1=\sqrt{43}~_{\sf CM}

Второй диагональ также ищем по т. косинусов

d_2^2=a^2+b^2-2ab\cos \beta\\ d_2^2=8^2+(7\sqrt{3})^2-2\cdot 8\cdot 7\sqrt{3}\cdot (-\frac{\sqrt{3}}{2})\\ d_2^2=64+147+168\\ d_2^2=379\\ d_2=\sqrt{379}~_{\sf CM}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
nimnogopozitiva nimnogopozitiva  09.06.2019 04:20
Найдите площадь равнобокой трапеции,если ее меньшее основание равно 18 см,высота 9 см,и острый угол равен 45 градусов...
raniskarimov2 raniskarimov2  09.06.2019 04:20
Один угол параллелограмма больше другого на 2. найдите больший угол параллелограмма...
Николь28071547 Николь28071547  09.06.2019 04:30
Дана правильная треугольная пирамида. стороны основания 6. боковые ребра 8. чему равна сумма углов при вершине пирамиды? есть ли какое-нибудь свойство?...
Сауле121 Сауле121  09.06.2019 04:30
Дан параллелепипед abcda1b1c1d1.медианы треугольника aсd1 пересекаются в точке m. разложите вектор вм по векторам а = ва, b= вв1, c = вс....
Юлик334 Юлик334  09.06.2019 04:30
Жк монитор имеет форму четырехугольной прямой призмы.определите площадь поверхности экрана монитора и выясните площадь боковой поверхности корпуса монитора.параметры...
Кариночка346 Кариночка346  09.06.2019 04:30
Площадь параллелограмма равна 120. точка е - середина стороны сд. найдите площадь трапеции абед....
мангл63 мангл63  09.06.2019 04:30
Впрямоугольной трапеции большая диагональ является биссектрисой острого угла и равна 8, а расстояние от вершины тупого угла до этой диагонали равно 3. найдите площадь...
MariaRils MariaRils  16.02.2021 09:46
2. В треугольнике АВС угол С прямой, АС = b, ZA = а. Выразите AB, BC, ZB через Биа. Найдите их значения, если ЗА...
kostan555ua kostan555ua  16.02.2021 09:47
ТОЛЬКО ДАВАЙТЕ БЕЗ НЕЗНАЮ ЕСЛИ НЕ ЗНАЕТЕ ПРОХОДИТЕ МИМО​...
bon1101 bon1101  16.02.2021 09:49
Дано KL||MN; OL =3см LN=6см ;OK=2см . Знайти K M​...

Популярные вопросы