Воснове прямой призмы лежит прямоугольный треугольник, гипотенуза которого равна 13 см, а один из катетов 12 см. найти объем призмы, если ее высота равна 5 см. в основі прямої призми лежить прямокутний трикутник, гіпотенуза якого дорівнює 13 см, а один з катетів 12 см. знайти об'єм призми, якщо її висота дорівнює 5 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Кто открыл пролив между азией и америкой?...
1 - Объясните что превращению сша после второй мировой войны в лидера...
2 - Ну-ка, , . каковы основные факторы размещения растениеводства...
3 - Какие ответы на вопросы что такое счастье? и приносит ли счастье...
3 - Почему в слове экскурсионный пишится о...
3 - Пропен относится к: 1) алканам 2) алкенам 3) алкинам 4) циклоалканам...
2 - Синтаксичний розбір речення. попросили бога зробити ім кожушки...
2 - Распредели слова по группам. с соединительной буквой о и с соединительной...
2 - 1.укажите неверное утверждение. а) сложным называется предложение,...
1 - Калканам относится: 1) бутадиен-1,3 2) бутан 3) бутен-2 4) бутин-1...
3
По теореме Пифагора находим второй катет:
Значит катеты равны 5см и 12 см.
Обьем призмы равен площадь основы на высоту:
V=Sосн*H(где H-высота призмы)
H=5см,
Sосн=1/2*AB*AC,где AB и AC-длины катетов
по теореме Пифагора найдем длину второго катета AB= (BC-гипотенуза)
(BC-гипотенуза)
AB=5cм
Sосн=1/2*5*12=30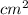 .
.
V=30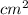 *5см=150
*5см=150