Восновании прямой призмы лежит ромб с острым углом 60 градусов и стороной 6 сантиметров найдите меньшую диагональ призмы если ее боковое ребро равно 8 сантиметров
Ответы
Если нарисовать рисунок, то видно, что необходимое нам расстояние является гипотенузой треугольника, катетами которого являются боковая сторона призмы и меньшая диагональ ромба. Боковая сторона по условию равна 8, значит нужно найти только диагональ ромба. Нарисуем в ромбе обе диагонали, они пересекаются под прямым углом, причём половина необходимой нам диагонали лежит против угла равного 30°. Отсюда находим длину диагонали ромба 6, а длина диагонали призмы равна 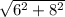 = 10
= 10
ПОКАЗАТЬ ОТВЕТЫ
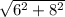 = 10
= 10
Другие вопросы по теме Геометрия
Популярные вопросы
- Вроссии четверть мировых лесных ресурсов. наша страна является крупным поставщиком...
3 - Как перевести 3дм квадратных и 10см квадратных...
2 - Округлите число 22.608 до единиц о объясните как...
1 - Туристы дошли до назначенного пункта за два дня. за первый день они на 3/7пути...
2 - Автомат получает на вход четырёхзначное десятичное число. по полученному числу...
2 - Вкниге 180 страниц. мальчик прочитал 30. какую часть книги прочитал мальчик....
3 - Найдите наибольший общий делитель чисел 133 и 228...
1 - Корень 121 умноженный на 44 деленный на x, равен корню 64 умноженного на 30,25,...
1 - 1. у кукурузы темная окраска доминирует над светлой а удлиненная форма над...
1 - Напишите вместо точек нужное слово (вариант в скобочках): 1) i monkey at the...
1