Вокруг треугольника АВС описана окружность. Точки М, N, К
соответственно - средины дуг АВ, ВС, АС, на которые точки А, В, С делят
окружность. Докажите, что отрезки MN и ВК перпендикулярны.

Пусть L-точка пересечения MN и BK.

∪KAC=∪KCN

их сумма равна π

От сюда их полусуммы тоже равны и KLM=KLN=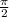

BK-диаметр, а любой угол, опирающийся на диаметр - прямоугольный, отсюда ∠KLM=90°, отсюда BK⊥MN

(надеюсь, что я правильно сделал, ибо сам жестко туплю)

Добрый день, я буду рад помочь вам разобраться с этим математическим вопросом.

Чтобы доказать, что отрезки MN и ВК перпендикулярны, нам нужно воспользоваться свойствами окружностей и треугольников.

Давайте начнем с геометрической схемы проблемы:

A
/ | \
/ M N \
/___|____\
B C
| |
K V

Согласно условию, точки M, N и К - это средины дуг АВ, ВС и АС, на которые точки А, В и С делят окружность. Поэтому длины дуг АМ, МВ, ВН, НС, СК и КА равны.

Шаг 1: Докажем, что треугольник АВК равносторонний.

Так как дуги АМ и АК равны, углы АМК и АКМ равны по свойству равных дуг. Но также в треугольнике АМК углы АМК и АКМ являются углами треугольника, а значит, они равны. Оба этих угла равны 60 градусам, поэтому треугольник АМК является равносторонним.

Шаг 2: Докажем, что отрезки ВН и МК равны.

Поскольку дуги МВ и ВК равны, углы МВК и ВМК равны, так как они соответствуют равным дугам. Углы МВК и ВМК вместе составляют 120 градусов, что является суммой углов треугольника. Следовательно, угол КМВ равен 180 - 120 = 60 градусов. Но мы установили, что углы треугольника АМК равны 60 градусам каждый, поэтому уголов КМВ и АМК равны. Таким образом, треугольники КМВ и АМК подобны по двум сторонам и углу, а значит, их стороны пропорциональны.

Теперь у нас есть все предпосылки, чтобы доказать, что отрезки MN и ВК перпендикулярны.

Шаг 3: Докажем, что отрезки MN и ВК перпендикулярны.

Для этого нам нужно показать, что угол ВКМ равен 90 градусам.

У нас уже есть два равных прямогольника (равносторонних треугольника): АМК и КМВ.

Угол КМВ равен 60 градусам, так как это угол равностороннего треугольника АМК.

Угол КМВ равен углу КАВ, так как это уголы между равными дугами.

Также угол ВКМ равен равностороннему треугольнику КМВ, так как этот треугольник равен по двум сторонам и углу треугольнику АМК.

В итоге, мы получили, что угол ВКМ равен 60 градусам и равносторонний треугольник КМВ. Но 60 градусов + 90 градусов (так как треугольник с прямым углом) = 150 градусов. Однако сумма углов треугольника должна быть 180 градусов, что означает, что угол ВКМ равен 180 - 150 = 30 градусов.

Поскольку мы получили, что угол ВКМ равен 30 градусам, а прямой угол равен 90 градусам, то отрезки MN и ВК перпендикулярны.

Я надеюсь, что это решение ясно и понятно. Если у вас возникнут дополнительные вопросы, буду рад помочь.