1. Геометрия
  2. Вокруг шара описан усеченный

Вокруг шара описан усеченный конус. радиусы усеченного конуса относятся как 4: 9. радиус шара равен 6 см. найдите площадь осевого сечения конуса.

Dddgirl777 Dddgirl777    2   04.06.2019 21:11    3

Ответы
VoltGame VoltGame  01.10.2020 19:26

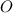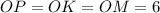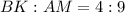Пусть шар с центром в точке O и радиусом OP = OK = OM = 6 см вписан в усеченный конус, у которого радиусы оснований относятся как BK : AM = 4 : 9.

Пусть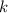 k — коэффициент пропорциональности. Тогда 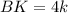BK = 4k, а AM = 9k

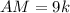
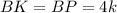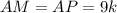По свойству касательных: отрезки касательных проведенных из одной точки, равны. Значит, BK = BP = 4k и AM = AP = 9k.

Проведем высоту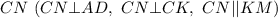 CN \ (CN \bot AD, \ CN \bot CK, \ CN || KM)

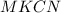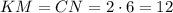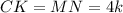
Тогда четырехугольник MKCN является прямоугольником со сторонами KM = CN = 2 \cdot 6 = 12 см и CK = MN = 4k

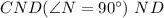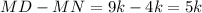
Следовательно, катет прямоугольного треугольника CND (\angle N = 90^{\circ}) \ ND равен MD - MN = 9k - 4k = 5k

Если трапеция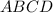 ABCD равнобокая значит,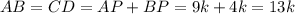 AB = CD = AP + BP = 9k + 4k = 13k

Рассмотрим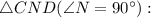 \triangle CND (\angle N = 90^{\circ}):

По теореме Пифагора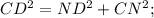 CD^{2} = ND^{2} + CN^{2};

(13k)^{2} = (5k)^{2} + 12^{2}\\169k^{2} = 25k^{2} + 144\\144k^{2} = 144\\k^{2} = 1

k = 1

k = -1 — не удовлетворяет условию задачи

AD = 2AM = 2 \cdot 9k = 18k = 18 \cdot 1 = 18 см

BC = 2BK = 2 \cdot 4k = 8k = 8 \cdot 1 = 8 см

Площадь осевого сечения конуса — это площадь трапеции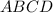 ABCD

S = \dfrac{BC + AD}{2} \cdot MK = \dfrac{8 + 18}{2} \cdot 12 = 156 см²

ответ: 156 см²


Вокруг шара описан усеченный конус. радиусы усеченного конуса относятся как 4: 9. радиус шара равен
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
darkhanio darkhanio  10.06.2019 01:50
Отметьти в тетради точки а и с.проведите через них прямую.отметьте на прямой ас еще три точки и обозначти их.отметьти четыри точки,не лежащие на прямой ас ; обозначти...
lizaroma224 lizaroma224  10.06.2019 01:50
Решить, : з abcd - параллелограмм ab = 2 см св = 3 см угол a = 60 градусов найти: ac, bc, s abcd и h....
Максим215281 Максим215281  11.09.2019 18:50
Даны вектора a(0; 2; -2) и b(1; 2; 3). найдите косинус угла между ними....
Dizelshop Dizelshop  11.09.2019 18:50
Вромбе mpkt диагонали равны 48 см и 14 см, а высота 25 см. найдите площадь ромба и его сторону...
1244ррровг 1244ррровг  11.09.2019 18:50
Высота цилиндра равна 6 см,а площадь его осевого сечения равна 48см². найдите площадь его полной поверхности....
rom4il rom4il  11.09.2019 18:50
Лан треугольник abc. a(1; -3; 0) b(3; 0; 4) c(0; 1; 3). найдите длину медианы проведенной из вершины а....
angelina140817 angelina140817  11.09.2019 18:50
Высота равнобедренного треугольника 5см основания 24см чему. равно боковые стороны...
kasoimandarin1 kasoimandarin1  11.09.2019 18:50
Даны точки a(0; 3; -2) b(4; -1; 7) c(2; -2; 0) найдите координаты ac,ba...
Александр756 Александр756  11.09.2019 18:50
Даны точки с(2; 7) и е(-3; 5). найдите координаты вектора се...
xeniathcelykh xeniathcelykh  23.08.2020 00:30
В равнобедренном треугольнике длина основания равна 30 см, длина высоты, проведенной к основанию, — 20 см. Определить длину высоты, проведенной к боковой стороне....

Популярные вопросы