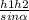Висоти паралелограма дорівнюють h1і h2, а кут між ними - а. визначити площу паралелограма.
Другие вопросы по теме Геометрия
Популярные вопросы
- Заполните таблицу. Какова урожайность большинства хозяйств? Урожайность зерновых...
3 - Кінці відрізка АВ завдовжки 17 см лежать на двох паралельних площинах, відстань...
2 - Write an essay on the theme: My favourite food ...
3 - 11 Spell the words. Example: [grəu] - grow1. [ kærət] -2. [vedsitəbl]3. [bar]4....
3 - О чем заставляет задуматься стихотворение И.А.Бунина Родина...
2 - розв язати задачу з хімії 9 клас обчислити масову частку карбону у пальмітиновій,...
1 - решите задачу с ОДНОГО уравнения, А НЕ СИСТЕМЫ . разность двух чисел равна 34,...
2 - 4 класс задание впринципе легкое ...
2 - Стислий переказ будь ласка на завтра треба❤і складний план до нього!дякую❤...
2 - 5) Решите систему неравенств (решение + рисунок + ответ в виде числового 5х...
1
Высоты параллелограмма равны h1и h2, а угол между ними - а. Определить площадь параллелограмма.
Угол между высотами равен острому углу параллелограмма, т.к. их стороны и высоты перпендикулярны.
S = a*h2, определим сторону а = h1/sina
S = h1*h2/sina
Пусть дан параллелограмм ABCD, у которого проведены высоты ВК=h1 и DM=h2, точка О - точка пересечения высот,угол KOD=
Рассмотрим четырехугольник АМОК, у него угол АМО= углу АКО=90 градусов, угол МОК=180- , то угол МАК=180-(180-
, то угол МАК=180-(180- )=
)=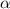
Из треугольника АВК по определению синуса: АВ=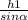
S=AB*h2=