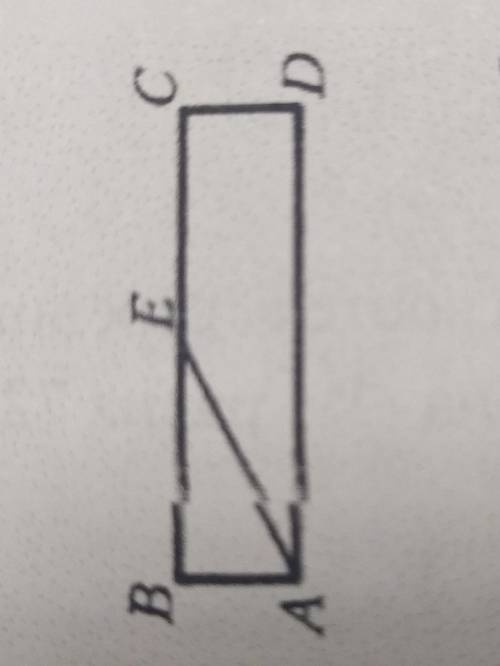
Вершина А прямоугольника соединили с серединой стороны ВС , причем соsугла АЕВ =0.8 . Найдите его площадь , если АВ =√2
Другие вопросы по теме Геометрия
Популярные вопросы
- Вставить артикли first animal can run. 2.have you pet? 3.i have got two...
1 - Сочинение на тему дикие животные должны быть защищены . ( 5 предложений...
1 - Решение петя нашёл в лесу в 5 раз больше грибов чем юра когда петя пересчитал...
1 - Чью судьбу (маши или владимира) вы считаете более несчастной и почему?...
1 - По технологии . нам задали творческий проект. я выбрала тему: кулинария....
3 - На тело действует сила тяжести 539h . чему равна масса тела?...
2 - Иллюстрация художника джона тенниела к сказке алиса в стране чудес - её...
3 - К400г раствора с массовой долей сульфата железа3 5% прилили 200г раствора...
3 - Напишите объёмы добычи, экспорта, импорта и потребления нефти для следующих...
2 - 7класс. россии назовите главную особенность политики петра 1 в области...
2
Также нам дано значение угла АЕВ, которое равно 0.8 радиан. И нам известна длина стороны АВ, которая равна квадратному корню из 2.
Мы должны найти площадь прямоугольника.
Давайте начнем решать эту задачу.
Во-первых, давайте найдем длину стороны ВЕ. Для этого мы можем использовать тригонометрию.
Мы знаем, что тангенс угла АЕВ равен противоположному катету (ВЕ) деленному на прилежащий катет (ВА). Таким образом, тангенс 0.8 радиан равен ВЕ/ВА.
Мы знаем, что ВА = √2, так что мы можем заменить это значение и решить уравнение:
тан(0.8) = ВЕ/√2
Теперь давайте решим это уравнение. Сначала умножим обе части уравнения на √2:
√2 * тан(0.8) = ВЕ
Находим приближенное значение выражения √2 * тан(0.8) с помощью калькулятора:
√2 * тан(0.8) ≈ 1.273
Таким образом, ВЕ ≈ 1.273.
Теперь мы можем найти площадь прямоугольника, зная длины его сторон. Площадь S прямоугольника равна произведению длин его сторон:
S = ВА * ВЕ
Мы знаем, что ВА = √2 и ВЕ ≈ 1.273, поэтому мы можем заменить эти значения и вычислить площадь:
S = √2 * 1.273 ≈ 1.799
Таким образом, площадь прямоугольника примерно равна 1.799.