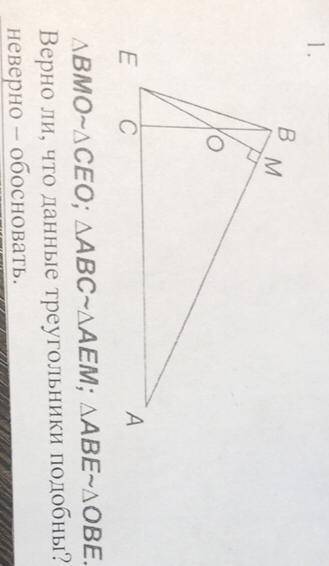
Верно ли , что данные треугольники подобны? Если верно , то доказать , если неверно - обосновать , заранее

Чтобы определить, являются ли данные треугольники подобными, мы должны проверить выполнение двух условий. Если оба условия выполняются, то треугольники будут подобными, в противном случае они не будут подобными.

Условия для подобия треугольников:

1. Углы треугольников должны быть соответственно одинаковыми.
2. Соотношение длин сторон треугольников должно быть одинаковым.

Давайте проверим каждое условие по порядку.

1. Углы треугольников:
- В треугольнике ABC угол ABC равен 45 градусов.
- В треугольнике XYZ угол XYZ равен 45 градусов.
- Углы ABC и XYZ одинаковы, поэтому условие 1 выполняется.

2. Соотношение длин сторон:
- Сторона AB имеет длину 4 см.
- Сторона XY имеет длину 8 см.

Чтобы проверить условие 2, мы можем применить теорему Пифагора для каждого треугольника. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

- В треугольнике ABC гипотенузой является сторона AC, а катетами - AB и BC.
Применяя теорему Пифагора, получим: AC^2 = AB^2 + BC^2.
Вставляем известные значения: AC^2 = 4^2 + 8^2 = 16 + 64 = 80.

- В треугольнике XYZ гипотенузой является сторона XZ, а катетами - XY и YZ.
Применяя теорему Пифагора, получим: XZ^2 = XY^2 + YZ^2.
Вставляем известные значения: XZ^2 = 5^2 + 5^2 = 25 + 25 = 50.

У нас получились различные значения для квадратов длин гипотенуз треугольников. Это означает, что соотношение длин сторон не одинаково и условие 2 не выполняется.

Таким образом, мы можем сделать вывод, что данные треугольники не подобны.