векторы) в треугольнике авс ав=6 вс=8
Другие вопросы по теме Геометрия
Популярные вопросы
- Подметём разобрать по составу. заранье огромное ....
3 - Плотностью вещества называется величина, ....
2 - Из ружья сделали 30 выстрелов, при этом было совершено 6 промахов....
2 - Знайти спільнокореневі слова до слів дорогий, дорога, подорожник,...
1 - Подготовить сообщения о дружбе народататарстана...
1 - Сколько чисел находится между числами 48 и 95...
2 - Заранее столицей своих земель князь олег объявил: а) новгород...
3 - Какие вечные проблемы поднимает шекспир в трагедии ромео и джульетта...
2 - 3. найдите значение выражения: 287 * 8 + (14 665 - 7 567) =...
3 - Какой объем воды может откачать за 1 час насос мощность 50квт...
3
а). Так как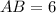 и
и 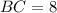 , то
, то 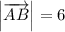 и
и 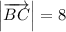 .
.
Получается, что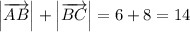
б). Для сложения двух векторов воспользуемся формулой:
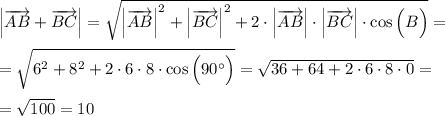
ответ: 14; 10 .Модуль вектора это его длина (расстояние от начала до конца).
ΔABC - прямоугольный (∠В=90°).
Найдём AC, гипотенузу ΔABC, по теореме Пифагора:
AC² = AB²+BC² = 6²+8² = 36+64 = 100 = 10²
AC = 10
ответ: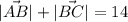 и
и 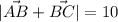 .
.