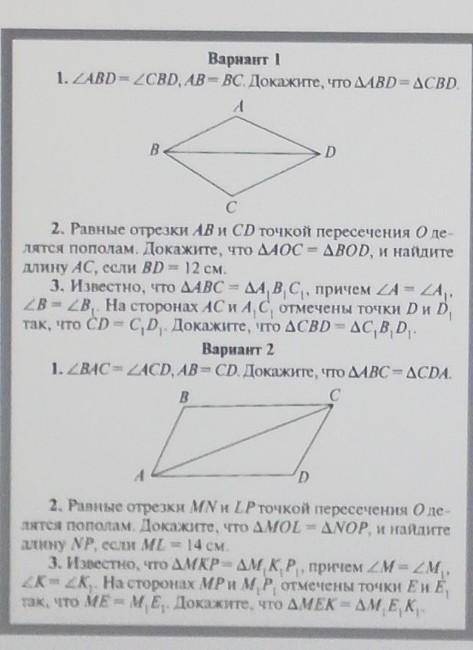
Вариант 1 1. ZABD=2CBD, AB = BC. Докажите, что ДABD=ACBD.
А A
B
D
T
C
2. Равные отрезки AB и CD точкой пересечения О де-
лятся пополам. Докажите, что ДАОС = ABOD, и найдите
длину AC, если BD = 12 см.
3. Известно, что ДАВС = A, B, C, причем ZA = 2A,
ZB = ZB. На сторонах AC и AC, отмечены точки D и D,
так, что CD = CD. Докажите, что ACBD - ACB, D.
Вариант 2
1.ZBAC= 2ACD, AB = CD. Докажите, что ДАВС = ACDA.
в
2. Равные отрезки MN и LP точкой пересечения Оде-
Лятся пополам. Докажите, что AMOL = ANOP, и найдите
длину NP, если MI = 14 см.
3. Известно, что ДМКР – ДМ КР, причем 2M = ZM
2K = 2К,. На сторонах MP и MP, отмечены точки Е и Е,
так, что ME – М. Е. Докажите, что AMEK = ДМ ЕК.​

Добрый день! Давайте рассмотрим каждый из вариантов по очереди и найдем решение к каждому из заданий.

Вариант 1:

1. У нас дано, что ZABD = 2CBD и AB = BC. Нам нужно доказать, что DABD = ACBD.
Для начала, обратим внимание на равенство ZABD = 2CBD. Заметим, что AB = BC и ZABD = CBD, значит, треугольники ZABD и 2CBD равны. Теперь рассмотрим треугольники DABD и ACBD. В них у нас уже есть равенство ZABD = 2CBD, а также AB = BC. Значит, по теореме о равенстве угловых сторон треугольника, треугольники DABD и ACBD также равны. Это и означает, что DABD = ACBD.

2. У нас дано, что AB и CD - равные отрезки, которые делятся пополам точкой О. Мы должны доказать, что ДАОС = ABOD и найти длину AC, если BD = 12 см.
Поскольку AB и CD делятся пополам точкой О, то это значит, что AO = OB и CO = OD. Мы знаем также, что AB = CD.
Для начала, докажем, что ДАОС = ABOD. Заметим, что у нас AO = OB и AB = CD. Таким образом, у нас есть равные противоположные стороны углов ДАОС и ABOD, значит, эти углы равны.
Чтобы найти длину AC, найдем длину AO. Поскольку AO = OB и BD = 12 см, то AO = AB - BO = AB - BD = AB - 12 см. Затем, поскольку AB и CD делятся пополам точкой О, то это означает, что AO = CO = AB/2. Таким образом, мы можем записать уравнение AO = AB/2 = AB - 12 см. Решим это уравнение:
AB/2 = AB - 12 см
AB - 2AB = -24 см
-AB = -24 см
AB = 24 см
Таким образом, мы нашли, что длина AB равна 24 см, а значит, длина AC также равна 24 см.

3. У нас дано, что ДАВС = A, B, C, а также ZA = 2A и ZB = ZB. На сторонах AC и AC, отмечены точки D и D, так, что CD = CD. Мы должны доказать, что ACBD - ACB, D.
Для начала, обратим внимание на равенства ZA = 2A и ZB = ZB. Заметим, что они нам мало дают информации, поэтому они пока могут быть нам не нужны.
Рассмотрим треугольники ACD и CBD. У нас есть равенство CD = CD, а также AB = BC. Исходя из этих равенств и из равенства AB = BC, мы можем сделать вывод, что треугольники ACD и CBD равны по теореме о равенстве угловых сторон треугольника. Теперь рассмотрим треугольники ACBD и ACB. У нас уже есть равенство ACD = CBD, а значит, мы получаем, что треугольники ACBD и ACB также равны по теореме о равенстве угловых сторон треугольника. То есть, ACBD = ACB.

Вариант 2:

1. У нас дано, что ZBAC = 2ACD и AB = CD. Нам нужно доказать, что ДАВС = ACDA.
У нас есть равенство ZBAC = 2ACD и AB = CD. Заметим, что ZBAC = ZACB и поскольку AB = CD, то треугольники ABZ и CDA также равны по теореме о равенстве угловых сторон треугольника. Теперь рассмотрим треугольники ACDA и ACB. У нас уже есть равенство ABZ = CDA, а значит, треугольники ACDA и ACB равны по теореме о равенстве угловых сторон треугольника. То есть, ДАВС = ACDA.

2. У нас дано, что MN и LP - равные отрезки, которые делятся пополам точкой О. Мы должны доказать, что AMOL = ANOP и найти длину NP, если MI = 14 см.
Поскольку MN и LP делятся пополам точкой О, то это значит, что MO = OL и NO = OP. Мы знаем также, что MN = LP.
Для начала, докажем, что AMOL = ANOP. Заметим, что у нас MO = OL и MN = LP. Таким образом, у нас есть равные противоположные стороны углов AMOL и ANOP, значит, эти углы равны.
Чтобы найти длину NP, найдем длину NO. Поскольку NO = OP и MI = 14 см, то NO = NP - MO = NP - MI = NP - 14 см. Затем, поскольку MN и LP делятся пополам точкой О, то это означает, что NO = OL = MN/2. Таким образом, мы можем записать уравнение NO = MN/2 = MN - 14 см. Решим это уравнение:
MN/2 = MN - 14 см
MN - 2MN = -28 см
-MN = -28 см
MN = 28 см
Таким образом, мы нашли, что длина MN равна 28 см, а значит, длина NP равна 28 см.

3. У нас дано, что ДМКР - ДМКР, причем 2M = ZM и 2K = 2К. На сторонах MP и MP, отмечены точки Е и Е, так, что ME - М. Е. Мы должны доказать, что AMEK = ДМ ЕК.
У нас уже дано равенство ДМКР = ДМКР. Заметим, что оно нам мало даёт информации, поэтому пока мы не будем его использовать.
Рассмотрим треугольники MEP и MEP. У нас дано, что ME = М. Е. Мы знаем также про равенство MEP = MEP. Таким образом, треугольники MEP и MEP равны по теореме о равенстве угловых сторон треугольника. Теперь рассмотрим треугольники AMEK и ДМ ЕК. У нас уже дано равенство MEP = MEP, а значит, мы получаем, что треугольники AMEK и ДМ ЕК равны по теореме о равенстве угловых сторон треугольника. То есть, AMEK = ДМ ЕК.

Я надеюсь, что мои объяснения были подробными и понятными. Если остались какие-либо вопросы или нужно более подробное объяснение, пожалуйста, сообщите мне.