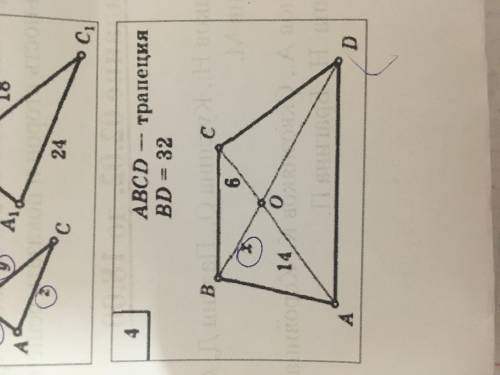
В задачах 1-4 найти длины отрезков x, y и z ABCD - трапеция, BD=32; CO=6; OA=14 (с отношением нужно) см. фото

Для решения данной задачи, мы можем использовать свойства трапеции.

1. Длина отрезка x:

На рисунке видно, что отрезок x проходит от вершины B до вершины C. Длина этого отрезка равна длине основания трапеции. Зная, что BD=32, мы можем заключить, что длина отрезка x равна 32.

Ответ: x = 32.

2. Длина отрезка y:

Отрезок y проходит от вершины B до точки O. Для вычисления длины этого отрезка, нам понадобится использовать свойство параллельных прямых и подобия треугольников.

В данной трапеции, параллельные стороны BC и AD имеют соотношение длин CO: OA = BC: AD.

Из информации в задаче, у нас есть CO=6 и OA=14.

Подставляя значения в формулу, получаем:

6:14 = BC: AD.

Для дальнейшего упрощения, мы можем поделить это соотношение на 2:

3:7 = BC: AD.

Теперь мы можем использовать свойство подобия треугольников. Так как BC и AD - параллельные стороны трапеции, то треугольники ABC и ADO подобны.

То есть, соответствующие стороны BC и AD имеют такое же отношение длин, как и соответствующие стороны AB и AO.

Зная, что AB=BC=32 (так как это боковая сторона трапеции) и AO=14, мы можем написать соотношение:

32:14 = BC: AD.

Решим это соотношение:

32/14 = BC/AD.

Упростим дробь:

16/7 = BC/AD.

Теперь мы можем подставить значение BC из первого задания (BC=32):

16/7 = 32/AD.

Для дальнейшего упрощения, мы можем умножить обе стороны равенства на 7:

16 = 32/AD.

Далее, умножим обе стороны равенства на AD, чтобы избавиться от деления:

16 * AD = 32.

Упростим уравнение:

AD = 32/16.

AD = 2.

Теперь мы знаем длину отрезка AD, который равен 2.

Ответ: y = 2.

3. Длина отрезка z:

Отрезок z - это отрезок AO, который проходит от вершины A до точки O. Мы уже знаем, что AO=14.

Ответ: z = 14.

Таким образом, длины отрезков x, y, и z равны:

x = 32,
y = 2,
z = 14.