В выпуклом четырехугольнике A
B
C
D
отмечена середина стороны
A
D
—
—
точка
M
. Отрезки
B
M
и
A
C
пересекаются в точке
O
. Известно, что ∠=65∘
∠
A
B
M
=
65
∘
, ∠=50∘
∠
A
M
B
=
50
∘
, ∠=100∘
∠
B
O
C
=
100
∘
, ∠=60∘
∠
A
D
C
=
60
∘
. Сколько градусов составляет угол
B
C
A
?
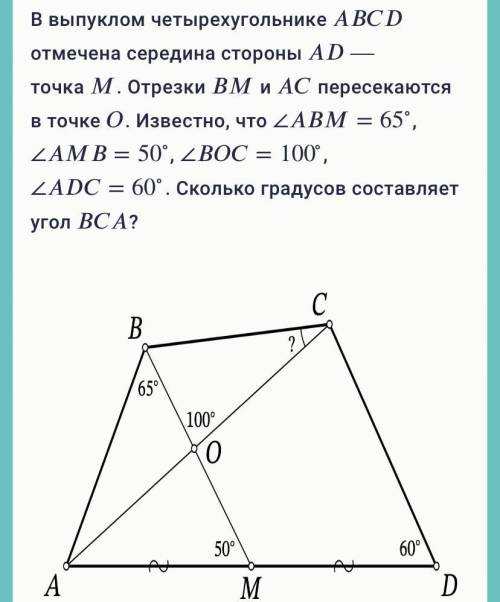
Другие вопросы по теме Геометрия
Популярные вопросы
- Как пишется (не)слышанный, (не)преодолимый, (не)умолкающие, (не)утомимый,...
2 - Лексикалык магынасы бар сөз a)ушін b)бөле c)дейін d)шейін...
3 - Социально- развитие в 20-50 годы 19 века кратко....
2 - Составь список авторов рассказов о животных расположите фамилии...
2 - To know why they are endangered a) am going b) will...
3 - Саставте 15 слов для диктанта с корнями: лаг, лож, рас, ращ, рост....
3 - Сочные растения силосуют для зимнего кормления скота, капусту —...
3 - Прочитайте отрывок из былины три поездки ильи муромца. определите,что...
2 - Верблюд может отложить в горбу жир который он использует затем при...
2 - (45356 - 6890) : 9 умножить на 350 - 9500...
1
25°
Объяснение:
Дано: ABCD - выпуклый четырехугольник.
∠АВМ=65°; ∠АМВ=50°; ∠ВОС=100°; ∠АDC=60°.
Найти: ∠ВСА.
1. Рассмотрим ΔАВМ.
Сумма углов треугольника равна 180°.
⇒ ∠А=180°-(∠АВМ+∠АМВ)=180°-(65°+50°)=65°
⇒ ΔАВМ - равнобедренный (углы при основании равны)
АМ=МВ.
2. Рассмотрим ΔАОМ.
Вертикальные углы равны.
⇒∠ВОС=∠1=100°
∠2=180°-(∠1+∠ОМВ)=180°-(100°+50°)=30°
3. Рассмотрим ΔАСD
∠АСD=180°-(∠2+∠D)=180°-(30°-60°)=90°
⇒ ΔАСD прямоугольный.
СМ - медиана (АМ=МD)
В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
⇒ АМ=МС=MD
4. Рассмотрим ΔАСМ.
АМ=МС (п.3) ⇒ ΔАСМ - равнобедренный.
⇒ ∠2=∠3=30° (углы при основании р/б треугольника равны)
∠АМС=180°-(∠2+∠3)=180°-60°=120°
5. Рассмотрим ΔВМС.
АМ=МВ (п.1)
АМ=МС (п.3)
⇒МВ=МС ⇒ΔВМС - равнобедренный.
∠5=∠ВСМ (углы при основании р/б треугольника равны)
∠4=∠АМС-∠АМВ=120°-50°=70°
⇒ ∠5=∠ВСМ=(180°-∠4):2=(180°-70°):2=55°
6. ∠ВСА=∠ВСМ-∠3=55°-30°=25°