В треугольнике высота, равная 4, делит основание в отношении 1:2. Найдите основание треугольника, если радиус вписанной окружности равен 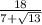
Другие вопросы по теме Геометрия
Популярные вопросы
- Посадвьте глагол в скобках в правильную форму (Present Perfect...
2 - 1. Дібрати до поданих слів форму або спільнокореневе слово, щоб...
3 - МОЖНО С ИНЕТА, 10 предложений туда должны входить все самое важное...
2 - Які гуманістичні ідеї прославляє Еразм Роттердамський у «Похвальному...
2 - Яка країна стала зразком європейського абсолютизму?...
2 - У треугольника АВС: угол АВС = 21 °; BAC = 69 . Прямая BL перпендикулярна...
1 - Молекулярни рівняння Zn(2+)+ SiO (2-)3=ZnSiO⬇️...
3 - Объясните расстановку знаков препинания в предложении. Хотя мы...
1 - С отрицания, дизъюнкции и конъюнкции постройте наиболее простое...
2 - РЕБЯТ ОЧЕНЬ КУЧА БАЛОВ -1/а(а+2)+1/(а+2)(а+4)+1/(а+4)(а+6)+1/(а+6)+1/(а+6)(а+8)=?...
2
Треугольник ABC, углы A B C, высота AE = h = 4; радиус вписанной окружности r = 18/(7 + √13) = (7 - √13)/2;
Ясно, что h/sinB + h/sinC + h(ctgB + ctgC) = 2p (периметр)
2S = 2pr = hr(1/sinB + 1/sinC + (ctgB + ctgC)) = h^2(ctgB + ctgC);
1/sinC + 1/sinB = (h/r-1)(ctgB + ctgC);
По условию ctgC=2ctgB; кроме того, 1/sinB = √(1 + (ctgB)^2); и также для C.
Пусть x = ctgB; a = h/r - 1; тогда
√(1 + 4x^2) + √(1 + x^2) = 3ax;
уравнение решается элементарно.
√(1 + 4x^2) = 3ax - √(1 + x^2);
1 + 4x^2 = 1 + x^2 -6ax√(1 + x^2) + (3ax)^2;
(3a^2 - 1)x = 2a√(1 + x^2); и дальше еще раз возвести в квадрат, и уравнение решится само собой.
Но на самом деле тут можно прерваться и вспомнить, что x = ctgB, откуда x/√(1 + x^2) = cosB = 2a/(3a^2 - 1); то есть фактически задача уже решена, надо только подставить числа и довести до формального ответа.
a = h/r - 1 = 4(7 +√13)/18 - 1 = (5 + 2√13)/9;
a^2 = (25 + 10√13 + 4*13)/81 = (77 + 20√13)/81;
3a^2 - 1 = (50 + 20√13)/27;
2a/(3a^2 - 1) = (2/9)*(5 +2√13)*27/(50 + 20√13) = 3/5;
Итак, cosB = 3/5; = > sinB = 4/5; => ctgB = 3/4.
Основание равно 3h*ctgB = 3*4*3/4 = 9;
Если сосчитать все, то получился треугольник со сторонами 9, 5 и 2√13; высота к стороне 9 равна 4 (по условию) и делит её на отрезки 3 и 6; отрезок длины 3 вместе с высотой 4 и стороной 5 образуют "египетский" треугольник 3,4,5. (Видимо, эта задача так и составлялась - взяли минимальный Пифагоров треугольник, продлили катет 3 за вершину прямого угла на удвоенную длинну, и получили условие.)
Легко проверить, что
площадь равна S = 9*4/2 = 18;
полупериметр p = (9 + 5 + 2√13)/2 = 7 + √13;
r = S/p = 18/(7 + √13);
Пусть дан треугольник АВС, высота BD = 4. r = 18/(7 + √13).
Примем AD = x, CD = 2x.
Тогда сторона основания АС = 3х.
Боковые стороны: АВ = √(16 + х²), ВС = √(16 + 4х²).
Периметр треугольника Р = 3х + √(16 + х²) + √(16 + 4х²).
Площадь треугольника S = (1/2)*4*3x = 6x.
Отсюда выразим периметр через площадь и радиус вписанной окружности:
P = 2S/r = 12x/(18/(7 + √13)) = 12x(7 + √13)/18 = 2x(7 + √13)/3.
Приравняем:
3х + √(16 + х²) + √(16 + 4х²) = 2x(7 + √13)/3.
Решение уравнения: х = 3.
ответ: основание АС = 3*3 = 9.