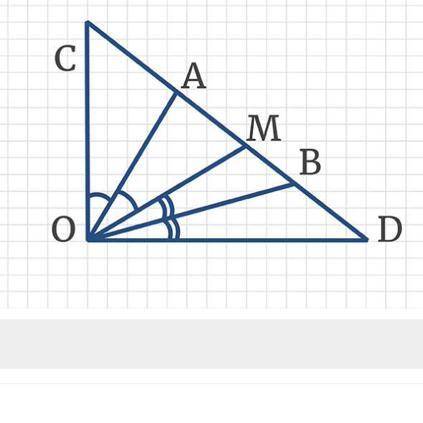
В треугольнике ODC ∠COD = 90°. Найдите ∠MOB, если OA – биссектриса угла ∠COM, при этом ∠COA = 20°, а BO – биссектриса ∠MOD.

40 градусов

Объяснение:

Если ОА биссектриса угла COM то значит она делит пополам

А так как нам известно что угол COA равен =20 то это половина угола COM которая она разделила, тоест мы просто умножаем на 2  и получаем 40

Для решения этой задачи нам понадобятся знания о свойствах биссектрис треугольника и о сумме углов треугольника.

В данной задаче у нас треугольник ODC, в котором ∠COD = 90°. Нам нужно найти угол ∠MOB.

Известно, что OA – биссектриса угла ∠COM, поэтому мы можем использовать свойство биссектрисы треугольника, которое гласит, что биссектриса делит противолежащий ей угол на две равные части. То есть ∠COA = ∠MOA = 20°.

Также известно, что BO – биссектриса угла ∠MOD. По свойствам биссектрис треугольника, мы можем сказать, что ∠MOB = ∠DOB.

Теперь нам нужно найти угол ∠DOB.
Обратим внимание, что треугольник ODC является прямоугольным треугольником, поэтому сумма углов треугольника будет равна 180°. То есть ∠CDO + ∠ODC + ∠COD = 180°.

У нас уже известно, что ∠COD = 90°. Заменим это значение в уравнении: ∠CDO + ∠ODC + 90° = 180°.

Учитывая, что ∠CDO = ∠COA и ∠ODC = ∠MOA, мы можем заменить эти значения в уравнении: ∠COA + ∠MOA + 90° = 180°.

Заменим известные значения: 20° + 20° + 90° = 180°.

Сложим значения: 20° + 20° + 90° = 130°.

Теперь мы знаем, что ∠COA + ∠MOA + 90° = 130°. Зная, что ∠MOA = 20°, мы можем найти значение ∠COA: ∠COA = 130° - 20° - 90°.

Выполняем вычисления: ∠COA = 130° - 20° - 90° = 20°.

Теперь мы нашли значение ∠COA, которое равно 20°.

Исходя из свойства биссектрисы, ∠COA = ∠MOA = 20°, поэтому ∠MOA = ∠MOB = 20°.

Таким образом, мы можем заключить, что ∠MOB = 20°.