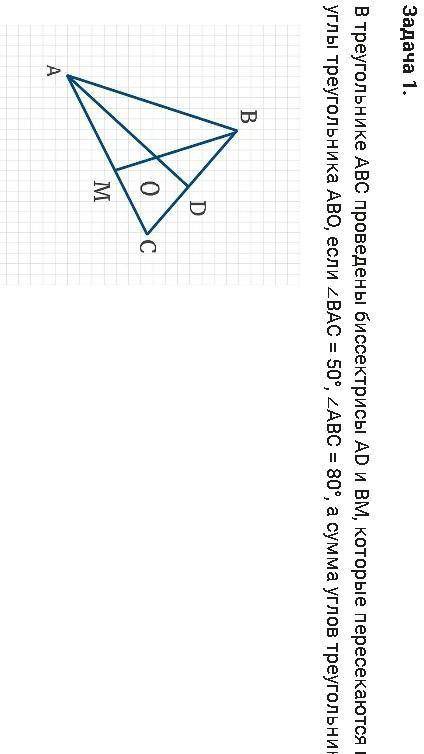
В треугольнике АВС проведены биссектрисы АD и ВМ , которые пересекаются в точке О. Найди углы треугольника АВО,если угол ВАС =50°, угол АВС = 80° , а сумма углов треугольника АВО равна 180° ​

Для решения этой задачи, давайте рассмотрим каждый угол треугольника АВО.

Первый угол - угол ВАО. Он образуется между отрезками ВА и ВО. Мы знаем, что биссектриса АD делит угол ВАС пополам, то есть угол ВАD равен 25° (половина угла ВАС). Также биссектриса ВМ делит угол АВС пополам, то есть угол ВМС равен 40° (половина угла АВС).
Теперь посмотрим на треугольник ВДС. Угл ВСД равен 180° - 50° (угол ВАС) - 40° (угол ВМС) = 90°.

Угол ВАО - это внутренний угол треугольника ВАД, а угол ВДА он равен 180° - 25° (угол ВАD) - 90° (угол ВСД) = 65°.

Следовательно, угол ВАО равен 65°.

Второй угол - угол АОВ. Он образуется между отрезками АО и ВО. Так как сумма углов треугольника АВО равна 180°, то угол АОВ равен 180° - угол ВАО - угол ВОА = 180° - 65° - 90° = 25°.

Таким образом, угол АОВ равен 25°.

Третий угол - угол АВО. Он образуется между отрезками АВ и ВО. Мы знаем, что сумма углов треугольника АВО равна 180°. Значит, угол АВО равен 180° - угол BAO - угол АОВ = 180° - 80° (угол АВС) - 25° (угол АОВ) = 75°.

Итак, угол АВО равен 75°.

Ответ: угол ВАО = 65°, угол АОВ = 25° и угол АВО = 75°.