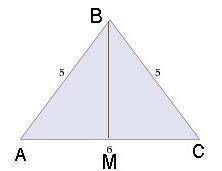
В треугольнике АВС медиана ВМ, равная 4 см, является высотой. биссектриса СN пересекает сторону ВМ в точке К Найдите: отрезок КМ

Поскольку ΔABC - равнобедренный, то BM - медиана, высота и биссектриса. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

KM = r.

AM = MC = AC/2 = 3 см. По теореме Пифагора (ΔABM):

BM = √(AB² - AM²) = 4 см

S = ah/2 = 6 * 4/2 = 12 см². С другой стороны S = pr

KM = r = S/p = 2S/P = 2*12/(5+5+6) = 1.5 см

ответ: 1.5 см.

Примечания: p - полупериметр треугольника, P - периметр тр-ка.