В треугольнике АВС АВ = 3, BC =3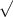2 ∠C = 30°. Найдите ∠A.

Чтобы решить эту задачу, мы можем использовать теорему синусов, которая гласит:

В треугольнике со сторонами a, b и c и противолежащими углами A, B и C, соответственно, справедлива формула:
a/sinA = b/sinB = c/sinC.

В нашем случае у нас есть сторона AB, которая равна 3, сторона BC, которая равна 3√2, и угол C, который равен 30°. Нам нужно найти угол A.

Мы можем использовать теорему синусов для отношения между сторонами и углами:
AB/sinA = BC/sinC.

Подставим известные значения:
3/sinA = 3√2/sin30°.

Мы знаем, что sin30° = 1/2, подставим это значение:
3/sinA = 3√2/(1/2).

Теперь, чтобы избавиться от деления на дробь, помножим обе стороны уравнения на sinA:
3 = 3√2/(1/2) *sinA.

Упростим выражение на правой стороне уравнения:
3 = 3√2 * (2/1) * sinA.
3 = 6√2 * sinA.

Теперь разделим обе стороны на 6√2:
3/(6√2) = sinA.

Упростим дробь на левой стороне уравнения:
1/(2√2) = sinA.

Чтобы найти sinA, мы можем использовать таблицу значений синусов и найти значение, которое соответствует 1/(2√2). По таблице, мы видим, что sin30° = 1/2, что эквивалентно 1/(2√2). Значит, sinA = sin30°.

Теперь найдем угол A. Мы знаем, что sinA = sin30°. Значит, угол A равен 30°.

Ответ: ∠A = 30°.