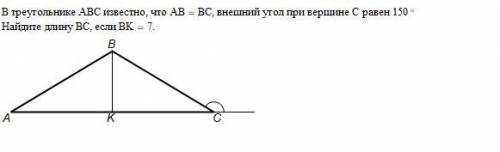
в треугольнике абс известно, что аб=бс. внешний угол при вершине с равен 150 найдите длину бс, если бк=7.

Для начала, давайте разберемся с данными условиями. В треугольнике АБС известно, что АБ = БС и внешний угол при вершине С равен 150 градусов. Также известно, что БК = 7.

Возьмем некоторую точку М на продолжении БС за точку С так, чтобы длина БС была равна длине СМ.

Мы можем заметить, что треугольники АБК и МКС являются равнобедренными, так как АБ = БК и МК = КС (по условию).

Теперь давайте найдем угол КМС. Известно, что сумма углов треугольника равна 180 градусов.

Угол между БК и СК равен углу КМС, так как треугольник АБК и треугольник МКС равнобедренные.

Таким образом, угол КМС = 180 - 150 = 30 градусов.

Также заметим, что треугольники АКМ и СКМ являются равнобедренными, так как АК = МК (по теореме о равных углах) и КМ = КС = БС (по условию).

Теперь мы можем использовать теорему синусов в треугольнике СКМ:

sin(КМС) / КМ = sin(КСМ) / СМ

sin(30) / 7 = sin(СКМ) / БС

sin(30) / 7 = sin(СКМ) / (АБ + БС) (так как АБ = БС)

sin(30) / 7 = sin(СКМ) / (БС + БС)

После этого мы можем преобразовать данное уравнение, чтобы получить значение БС:

sin(30) / 7 = sin(СКМ) / (2БС)

Переставим БС влево:

БС = (sin(СКМ) / (2 * sin(30))) * 7

Теперь мы можем найти sin(СКМ) с помощью теоремы синусов в треугольнике СКМ:

sin(СКМ) / БС = sin(90) / КС

sin(СКМ) / БС = 1 / БК (так как КС = БК, так как треугольник КСМ равнобедренный)

sin(СКМ) / БС = 1 / 7

Переставим БС влево:

sin(СКМ) = (1 / 7) * БС

Так как sin(90) = 1, мы можем записать:

sin(СКМ) = (1 / 7) * БС

Теперь мы можем подставить данное выражение для sin(СКМ) в уравнение для БС:

БС = ((1 / 7) * БС) / (2 * sin(30)) * 7

Упростим уравнение, умножив (2 * sin(30)) на 7:

БС = ((1 / (2 * sin(30))) * БС) * 7

Упростим дробь, заметив, что sin(30) = 1 / 2:

БС = (1 / (1 * 2)) * БС * 7

БС = (1 / 2) * БС * 7

БС = (1/2) * 7

БС = 3.5

Таким образом, длина БС равна 3.5.