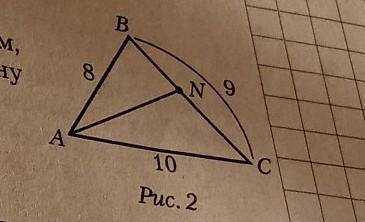
В треугольнике ABC (рис. 2) AC = 10 см, ВС = 9 см, AB = 8 см,
AN- биссектриса. Найдите длину отрезка CN​​

Хорошо, давайте решим эту задачу.

У нас дан треугольник ABC, где AC = 10 см, BC = 9 см и AB = 8 см. Мы также знаем, что AN - биссектриса треугольника ABC. Нам нужно найти длину отрезка CN.

Чтобы решить эту задачу, давайте вспомним некоторые свойства биссектрисы в треугольнике. Биссектриса треугольника делит противолежащие стороны на отрезки, пропорциональные друг другу.

Мы можем воспользоваться этим свойством, чтобы найти длину отрезка CN. Для этого нам понадобится найти пропорцию между отрезками CB и BN.

Для начала, обратим внимание на треугольник ABC. Мы знаем, что AC = 10 см, BC = 9 см и AB = 8 см.

Далее, давайте обратимся к теореме углового сектора.

Теорема углового сектора устанавливает, что биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам треугольника.

Применительно к нашей задаче, мы можем записать следующую пропорцию:

{{{BC/BN = AC/AN}}}

Подставляя известные значения, получим:

{{{9/BN = 10/AN}}}

Теперь у нас есть пропорция между отрезками BC и BN.

Далее, давайте обратим внимание на другую пропорцию. Нам нужно найти пропорцию между отрезками AN и CN.

Мы знаем, что AN - биссектриса. Значит, AN делит угол C на два равных угла.

Теперь, обратим внимание на треугольник ANC. Мы знаем, что углы ANC и BNC равны, так как они соответственные углы.

У нас есть две пары равных углов: углы ANB и BNC, углы ANC и BNC.

Таким образом, треугольники ANB и BNC подобны. Поэтому соответствующие стороны треугольников ANB и BNC пропорциональны.

Мы можем записать следующую пропорцию:

{{{AN/CN = BN/BC}}}

Подставляя известные значения, получим:

{{{AN/CN = BN/9}}}

Теперь у нас есть пропорция между отрезками AN и CN.

Мы уже знаем пропорцию между отрезками BC и BN:

{{{9/BN = 10/AN}}}

Теперь у нас есть две пропорции, и мы можем решить систему уравнений, чтобы найти значения AN и CN.

Подставим выражение для BN из первой пропорции во вторую пропорцию:

{{{AN/CN = (9/BN)/9}}}

Заметим, что вторая пропорция упрощается:

{{{AN/CN = 1/9}}}

Теперь мы можем установить равенство между пропорциями:

{{{1/9 = 10/AN}}}

Теперь нам нужно найти значение AN. Для этого мы можем использовать пропорцию:

{{{1/9 = 10/AN}}}

Перекрестное умножение даст нам:

{{{AN = 10*9}}}

{{{AN = 90}}}

Теперь у нас есть значение AN.

Далее, мы можем использовать это значение, чтобы найти значение CN.

Мы знаем, что AN/CN = 1/9. Подставляя известное значение AN, получаем:

{{{90/CN = 1/9}}}

Перекрестное умножение даст нам:

{{{CN = 90*9}}}

{{{CN = 810}}}

Таким образом, длина отрезка CN равна 810 см.

Это полное решение задачи. Если у вас есть ещё вопросы, я готов на них ответить!