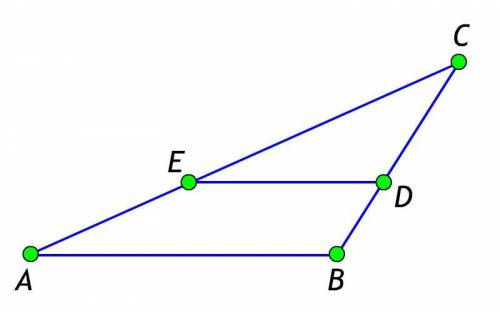
В треугольнике ABC провели отрезок ED так, что два треугольника оказались подобными. Определите, чему равна разность ∠ CAB – ∠ CED, если ∠ ACB = 48°, ∠ EDC – тупой.
∠ CAB – ∠ CED =?
Другие вопросы по теме Геометрия
Популярные вопросы
- Еще , сочинение на тему путь дом и произведение по вашему усмотрение!...
3 - Уводія було 50 літрів бензину він залив у бак автомобіля 35 літрів...
3 - Что послужило причинами и поводом к революции во франции 1830 года?...
1 - От деревни до города велосипедист ехал 4 ч со скоростью 12 км /ч...
2 - Почему клетку сравнивают с миниатюрной природной лабораторией ?...
3 - Состровом ! почему доктор ливси и hunter покинули корабль? 20 !...
3 - Определить массовую долю в процентах. 1)нитрат бария 2)ортофосфат...
2 - Постройте в одной системе координат графики ф-й y=-1/3x+1 ; y=-1/3x-2;...
3 - Купили 6м шовку, сатину у 2 рази більше, а сукна на3 менше ніж шовку...
2 - Речення зі словом-летіти або з летімо,лети,леті наперед дуже дякую:...
1
Перед тем, как начать решение, давайте вспомним некоторые определения.
Треугольники называются подобными, если соответствующие углы равны, а соответствующие стороны пропорциональны.
В данной задаче, нам дан треугольник ABC и точка E на стороне AB треугольника ABC.
Мы знаем, что ∠ACB = 48° и ∠EDC – тупой.
Поскольку треугольники ABC и EDC подобны, соответствующие углы должны быть равны.
Давайте рассмотрим углы, которые нам даны.
∠ACB равен 48°.
Теперь давайте найдем ∠CED.
Поскольку треугольник EDC подобен треугольнику ABC, углы ∠CED и ∠CAB должны быть равны.
Таким образом, ∠CED = 48°.
Теперь мы можем найти разность ∠CAB и ∠CED.
∠CAB = 48° и ∠CED = 48°, поскольку они должны быть равны.
Тогда разность ∠CAB – ∠CED равна:
∠CAB – ∠CED = 48° – 48° = 0°.
Таким образом, разность ∠CAB – ∠CED равна 0°.
Ответ: ∠CAB – ∠CED = 0°.
Я надеюсь, что эта подробная и пошаговая информация помогла вам понять решение этой задачи. Если у вас остались какие-либо вопросы, не стесняйтесь задавать их!