В треугольнике ABC провели DE∥AC. Известно, что:

D∈AB,E∈BC, AB= 17 см, DB= 8,5 см, AC= 14 см. Вычисли DE.

 

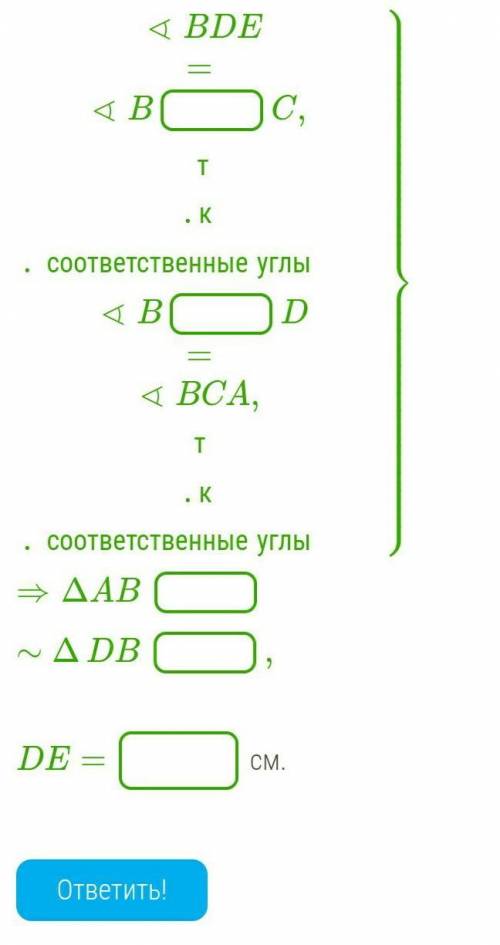
Сначала докажи подобие треугольников. (В каждое окошечко пиши одну большую латинскую букву.


​

Для начала, давайте докажем подобие треугольников.

Для этого нам понадобятся две пары соответственных сторон, которые пропорциональны. В данном случае, мы можем взять стороны AB и DE, а также стороны AC и DB.

По условию, AB=17 см и DB=8.5 см. Мы знаем, что сторона AB пропорциональна стороне DE, так как DE параллельна AC, а ВD - одна из диагоналей параллелограмма ABCD, то есть делит его на два равных треугольника ABC и BAD. Поэтому, отрезок DE должен быть пропорционален стороне AB.

Следовательно, можно написать пропорцию:
AB/DE = BD/DA

Для нахождения стороны DA, нам понадобится использовать теорему Пифагора. В треугольнике BAD, мы знаем стороны BA=17 см и DB=8.5 см, поэтому мы можем вычислить сторону DA:

DA = sqrt(BA^2 - DB^2)
DA = sqrt(17^2 - 8.5^2)
DA = sqrt(289 - 72.25)
DA = sqrt(216.75)
DA ≈ 14.72 см

Теперь мы можем подставить полученные значения в пропорцию:
17/DE = 8.5/14.72

Теперь найдем сторону DE:
DE = (17 * 14.72) / 8.5
DE ≈ 29.72 см

Итак, ответ: DE ≈ 29.72 см