В треугольнике ABC провели DE||AC. Известно, что:
D ∈ AB, E ∈ BC, AB = 14 см, DB = 1,4 см, AC = 8 см. Вычисли DE.
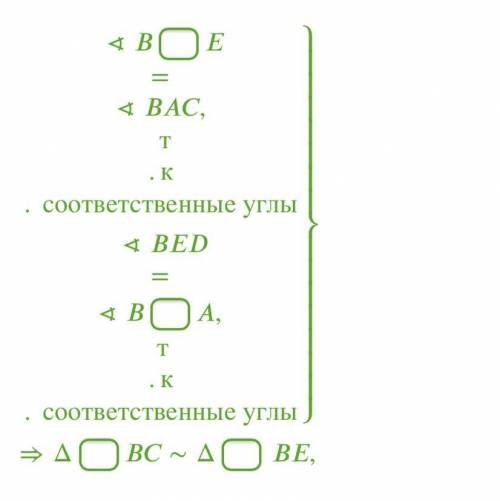
Сначала докажи подобие треугольников. (В каждое окошечко пиши одну большую латинскую букву.)
Другие вопросы по теме Геометрия
Популярные вопросы
- Придумайте рассказ об управлении Римской республикой от лица консула, народного...
1 - Что общего в занятиях, религии и культуре этрусков с историей известных...
3 - Почему царь Порсена отпустил Муция, который убил его казначея?...
3 - Чем отличалась власть первых римских царей от власти правителей государств...
3 - В чем своеобразие римской цивилизации? Какой след она оставила в мировой...
1 - Почему римляне отказались от власти царей и установили республику?...
2 - Составьте кроссворд «Мифы и легенды Древней Греции»...
3 - Кто занял господствующее положение в странах Западной Азии и в Египте?...
1 - Каковы были права и обязанности патрициев и плебеев в Древнем Риме?...
3 - Какие сказания о богах и героях Греции вы знаете? Какие качества в людях...
1
1. Дано: треугольник ABC, проведены отрезки DE и AC параллельно, где D ∈ AB, E ∈ BC, AB = 14 см, DB = 1,4 см, AC = 8 см. Нам нужно вычислить длину отрезка DE.
2. Докажем подобие треугольников ABC и ADE, используя два угла и одну сторону:
a) Угол AEB равен углу ABC (они оба соответственные углы);
b) Угол DEA равен углу BAC (они оба внутренние углы, образованные параллельными прямыми);
c) Сторона AB имеет пропорциональное соотношение с стороной AD (AB/AD = BE/DE, так как DE параллельна AC);
d) С учетом данных в условии, AB/AD = 14/1,4 = 10.
Из этих фактов следует, что треугольники ABC и ADE подобны по принципу "угол-угол-сторона" (УУС), что означает, что их соответствующие стороны пропорциональны.
3. Теперь мы можем использовать подобие треугольников, чтобы найти длину отрезка DE:
a) По подобию треугольников, имеем AB/AD = AC/AE;
b) Подставляя известные значения: 10 = 8/AE;
c) Решаем уравнение для AE: AE = 8/10 = 0,8 см.
Таким образом, длина отрезка DE равна 0,8 см.
Таким образом, мы доказали подобие треугольников ABC и ADE по принципу "угол-угол-сторона" и вычислили длину отрезка DE равной 0,8 см.