В треугольнике ABC его медианы AA1, BB1 и СС1 пересекаются в точке О. Середины отрезков OA, OB и OC обозначены соответственно A2, B2 и C2. Выразите периметр шестиугольника A2C1B2A1C2B1 через медианы ma = AA1, mb = BB1, mc = CC1.
Другие вопросы по теме Геометрия
Популярные вопросы
- Как делать звуко-буквенный разбор слова?...
1 - Представь частное t24: t6 в виде степени. выбери правильный ответ:...
3 - Определите элемент со схемой распределения электронов в атоме 2...
2 - Каковы различия между культурно- регионами? ,...
2 - Вчем отличатся природа предгорий и гор от природы степной полосы?...
3 - Мне перевести на язык: 1.я давно знаю билла. я знаю его 10 лет....
1 - Кількість теплоти, необхідну для нагрівання мідного тіла 50кг від...
2 - Теплоход по течению реки за 4 часа проплыл 124 км пути. сколько...
1 - 1. грибы признаками растений и признаками животных признаки царства...
1 - По белка и бурундук делят между собой найденную в лесу кучу орехов....
1
В треугольнике ABC его медианы AA1, BB1 и СС1 пересекаются в точке О. Середины отрезков OA, OB и OC обозначены соответственно A2, B2 и C2. Выразите периметр шестиугольника A2C1B2A1C2B1 через медианы ma = AA1, mb = BB1, mc = CC1.
Объяснение:
Медиана точкой пересечения делится на отрезки в отношении 2:1 ,считая от вершины ( см рисунок 1):
ОА=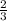 mа , ОВ=
mа , ОВ=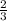 mb , ОС=
mb , ОС=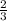 mc .
mc .
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон .Это отрезки :
А₂С₁ и А₁С₂ соответственно в ΔОАВ и ΔОАС ;
С₂В₁ и С₁В₂ соответственно в ΔОСА и ΔОАВ ;
А₂В₁ и А₁В₂ соответственно в ΔОАС и ΔОВС .
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
А₂С₁=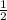 ОВ=
ОВ= 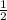 *
*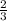 mb =
mb =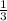 mb , А₁С₂ =
mb , А₁С₂ =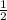 ОВ=
ОВ= 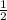 *
*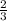 mb =
mb =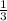 mb ;
mb ;
С₂В₁=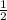 ОА=
ОА= 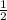 *
*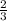 mа =
mа =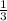 mа , С₁В₂ =
mа , С₁В₂ =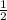 ОА=
ОА= 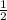 *
*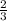 mа =
mа =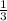 mа ;
mа ;
А₂В₁ =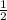 ОС=
ОС= 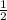 *
*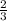 mс =
mс =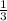 mс , А₁В₂ =
mс , А₁В₂ = 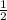 ОС=
ОС= 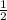 *
*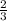 mс =
mс =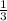 mс .
mс .
Р(шестиугольника)=2*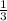 mb+2*
mb+2*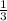 mа+2*
mа+2*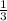 mс=
mс=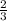 ( mа+ mb+mс)
( mа+ mb+mс)