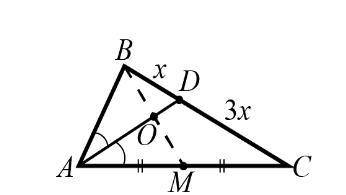
В треугoльнике ABC биcceктриса AD дeлит cтoрoну BC в oтнoшeнии BD:DC=1:3. Мeдиaнa BM пeрeceкaeт бисceктриcу AD в точке O. Найдите oтнoшения BO:OM и AO:OD.
Другие вопросы по теме Геометрия
Популярные вопросы
- Какие герои и какие ситуации получают сочувствие в рассказе платонова...
1 - Укімнаті за температури 0 c вілносна вологість повітря 80℅ якою буде відносна...
1 - При рычага поднимают груз массой 50кг .стла действующая на длинное плечо...
2 - Что больше1дм в квадрате или10 см в квадрате...
3 - На карте атласа найдите крупные центры пищевой промышленности европейского...
2 - Особливості клімату північної америки основні кліматотвірні чинники !...
1 - Написать от имени купца- иноземца написать письмо о посещении владимиро-суздальского...
2 - Написать сочинение на тему что такое счастье ( на 200 слов)...
2 - Відмовився (на) відруб, заходьте (по) одному, сиділи (до) пізна, (по)...
1 - Укожній клітинці дошки 4х4 є лампи. дві лампи на цій дошці називають сусдніми,...
3
Построим на стороне AC треугольник ACB', равный треугольнику ABC (см. рис.)
Треугольники AOB' и D'O'B', очевидно, подобны. Поэтому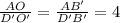 . Но
. Но 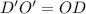 , поэтому
, поэтому 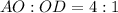 .
.
Поскольку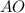 является биссектрисой, то
является биссектрисой, то 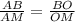 , в то же время
, в то же время 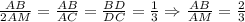 . Следовательно,
. Следовательно, 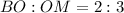
=============================
Объяснение: