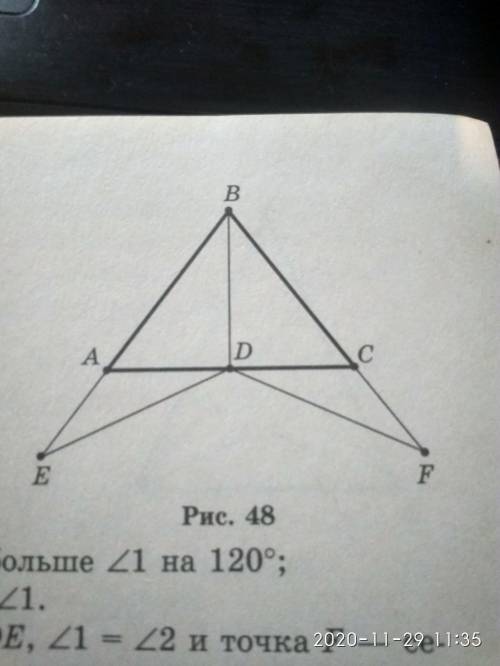
В треугольнике ABC AB=BC, отрезок BD - медиана. На лучах BA и BC (см. Рис.) Взяты соответственно точки E и F такие, что BE =BF. Докажите что: а) Треугольник ADE= треуг. CDF;
б)треуг. DEF - равнобедренный;
в) треуг. BDE = треуг. BDF
Другие вопросы по теме Геометрия
Популярные вопросы
- Укажите первый пароход переплывший атлантический океан в 1819 году...
3 - Кого из современных знаменитостей можно считать сильной личностью....
1 - Запиши родственные слова перо, пёрышко, оперение, перина, перистые...
3 - Окончания казахского языка по лицам...
3 - Какой род - эпос лирика или драма - чаще всего используются в нашей разговорной...
3 - Складіть по одному реченню з однорідними членамми,звертанням,вставним словом,дієприслівниковим...
3 - Какое проверочное слово к слову растут...
1 - Фанетическай разбор слова(буквенный разбор слова) сбил...
3 - Докажите почему человек это личность?...
1 - Сочинение на тему мой любимый герой...
3
а) треугольник АДЕ и СДФ имеют общую точку Д через них проходит прамая АС.
АД= ДС потому что медиана делит основу треугольника поровно. и БЕ равно БФ
Из этого выплывет, что АДЕ равен СДФ
б) по скольку АДЕ равен СДФ, значит ЕД равна ДФ.
и угол ДЕФ равен углу ДФЕ. Выходит, что треугольник ДЕФ равнобедренный
в) По скольку медиана делит основу треугольника АВС пополам и ВЕ равна ВФ, а АД равна ВС. значит, что треугольник АБД равен треугольнику ДБС. А треугольник АДЕ равен СДФ, выходит что ВДЕ равен ВДФ.
Объяснение:
готово.