В треугольниках ABC и A1B1C1 угол B = угол B1 ; AB/A1B1 = AC/A1C1 = 2/3
Если BC = 12, то B1C1 равна
а)6 б)18 в)3
Ну или же прост посмотрите на фотке всё)))
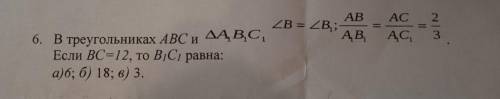
Популярные вопросы
- К многоатомным спиртам относится: полиэтилен метанол октан этиленгликоль...
3 - Индия занимает 2 -е место по численности населения в мире и является самым многонациональным...
2 - Чего не хочет видеть Раскольников в окружающем мире? Сочинение-рассуждение...
1 - Найти нужно лишнее в таблице...
2 - Реакцією нейтралізації добудьте солі CaS...
2 - ТЕРМІНОВО Складені розміщення з 10 елементів по 7. Скільки з цих розміщень: а)...
3 - Жарық жақсы шағылуы үшін дененің беті қандай болу керек?...
2 - Составит 2 во по тексты. 4. Мәтінді оқы. Бұл ертегі ме әлде аңыз ба? Ажыратып...
3 - Четырехугольник АВСD описан около окружности. АВ = 7 см, CD =11 см, ВС в два раза...
3 - Готуємось до тематичного оцінювання 4Тема: Вода1. Вибери твердження, що характеризує...
3
Первое свойство, которое мы можем использовать, гласит: если два треугольника подобны, то их соответствующие стороны пропорциональны.
В данной задаче треугольники ABC и A1B1C1 подобны по условию.
У нас есть следующая пропорция: AB/A1B1 = AC/A1C1 = 2/3
Теперь мы можем составить уравнения по этим пропорциям. Пусть x - длина стороны B1C1.
Тогда имеем следующее:
AB/A1B1 = AC/A1C1 = 2/3
AB/x = AC/x = 2/3
По свойству пропорций, мы можем умножить обе части уравнения на одинаковое число без изменения равенства. В данном случае, мы можем умножить обе части на x, чтобы избавиться от дробей:
AB = (2/3)*x
AC = (2/3)*x
Теперь нам нужно найти сторону BC. Из условия задачи, известно, что BC = 12.
Теперь мы можем использовать второе свойство подобных треугольников, которое гласит: если два треугольника подобны, то их соответствующие стороны имеют одинаковые отношения.
Используя это свойство, мы можем записать пропорцию:
BC/AB = B1C1/A1B1
Подставим известные значения:
12/(2/3)*x = x
12/(2/3) = 1
12*3/2 = 18
Таким образом, B1C1 равна 18.
Ответ: б) 18