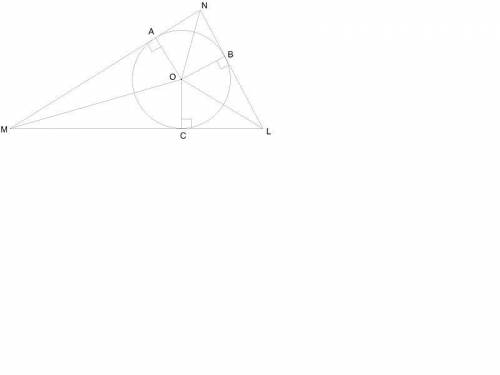
В треугольник вписана окружность. Вычисли неизвестные углы, если ∢ OMN = 26° и ∢ LNO = 29°. 12ok.png

∢ AOC =
°;

∢ AOB =
°;

∢ COB =
°.

Для решения данной задачи, нам понадобятся свойства треугольника, вписанного в окружность.

Первое свойство: если в треугольнике есть угол, опирающийся на хорду на окружности, то угол равен половине центрального угла, опирающегося на эту же хорду.

Исходя из данного свойства, у нас есть угол ∢OMN, опирающийся на хорду LN, следовательно, он равен половине центрального угла ∢LON. Так как значение предоставлено, ∢OMN = 26°, то половина центрального угла ∢LON равна 2 * 26° = 52°.

Также, у нас есть угол ∢LNO, опирающийся на эту же хорду LN, тогда его величина также будет равна половине центрального угла ∢BON. Значит, ∢BON = 2 * 29° = 58°.

Второе свойство: сумма углов в треугольнике равна 180°.

Теперь, мы можем рассмотреть треугольник OBN. Он содержит углы ∢AOC и ∢BOC. Чтобы найти эти углы, мы можем использовать свойство суммы углов в треугольнике.

Из этого следует:

∢AOC + ∢BOC + ∢OBM = 180°.

Так как ∢OBM является половиной центрального угла, опирающегося на ту же хорду LN, то его величина равна 52°.

Подставляем известные значения:

∢AOC + ∢BOC + 52° = 180°.

Теперь, нам необходимо найти ∢AOC и ∢BOC. Для этого используем второе свойство суммы углов в треугольнике.

Из треугольника OMA следует:

∢AOC + ∢OMA + ∢OAM = 180°.

Из треугольника ONA следует:

∢BOC + ∢ONA + ∢OAN = 180°.

Используя свойства суммы углов в треугольнике и значение углов, полученных ранее, мы можем записать следующие уравнения:

∢AOC + 26° + ∢OAM = 180°,

∢BOC + 29° + ∢OAN = 180°.

Теперь осталось найти значения ∢OAM и ∢OAN и решить уравнения.

Угол ∢OAM равен половине центрального угла, опирающегося на хорду AM. Так как ∢OMN равен 26°, то половина центрального угла равна 2 * 26° = 52°.

Угол ∢OAN имеет ту же самую величину, так как он опирается на ту же хорду AN.

Подставляем эти значения в уравнения:

∢AOC + 26° + 52° = 180°,

∢BOC + 29° + 52° = 180°.

Упрощаем и решаем уравнения:

∢AOC + 78° = 180°, ∢AOC = 102°,

∢BOC + 81° = 180°, ∢BOC = 99°.

Итак, получаем значения искомых углов:

∢AOC = 102°,

∢BOC = 99°.