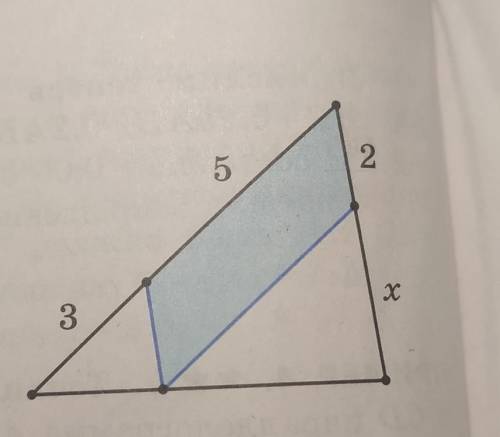
в треугольник вписали параллелограмм так как это показано на рисунке две вершины параллелограмма делят стороны треугольника на четыре отрезка три из которых имеют длины 3,5 и 2 найдите длину 4 отрезка
Другие вопросы по теме Геометрия
Популярные вопросы
- Сделать таблицу к . в 3 бочках по 280 л воды в каждой бочке, а в 12 ведрах...
2 - My parents are reading a book now. сделать 5 типов вопросов (отрицание,...
3 - Найдите площадь квадрат,сторона которого равна (2корень из 27+корень...
1 - Из города а и б находящихся на расстоянии 275 км в час друг от друга...
2 - Счего начать рассказ,как продолжить,,чем закончить...
3 - Напешите словосочитание по данной схеме. окончание имён существительных...
1 - Душевное возрождение князя андрея,его деятельность в питербурге...
2 - Відредагуйте речення. відвідувачі можуть зайти на протязі дня. наші працівники...
1 - Поезд был в пути 3 часа и км за первый час он км за второй на 20 км больше...
1 - Решите ( 5а⁴-2а²b⁴)²=? запишите в виде многочлена!...
3
1. Поскольку параллелограммы противоположных сторон равны, значит, BD = AC и AD = BC.
2. Последний отрезок, который нам необходимо найти (AB), является диагональю параллелограмма. Рассмотрим свойства диагоналей в параллелограммах:
- В последовательности параллелограммов, вписанных в треугольник, параллелограммы с одним углом будут иметь параллельные диагонали. Следовательно, мы можем сказать, что это верно для AB и BD.
- Отрезок AB дополняет и поперечной вектор BD до AC. Из первого свойства следует, что AB и AC параллельны.
- Отрезки AB и AC также имеют одну общую вершину (A).
3. Мы знаем, что треугольник делится на 4 части: AB, BD, DC и CA. Известно, что BD = AC = 3,5, AB = 2 и DC = 3.
Теперь мы можем решить задачу:
1. Отрезок BD = AC = 3,5.
2. Отрезок AB = 2.
3. Отрезок DC = 3.
Мы хотим найти длину отрезка AB. Поскольку AB параллельно DC, они оба являются линейными отрезками, попадающими в одну и ту же параллельную плоскость (базовую сторону параллелограмма).
Теперь мы можем использовать пропорции для нахождения длины AB:
AB/DC = BD/AC
Заменим известные значения:
AB/3 = 3.5/3
Остается только решить пропорцию:
AB = (3.5/3) * 3
AB ≈ 3.5
Таким образом, длина отрезка AB равна приблизительно 3.5.