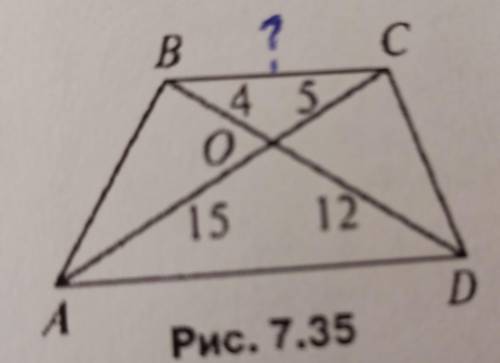
В трапеции: диагонали BD и АС пересекаются в точке О. ВО=4,СО=5,DO=12,АО=15. Найти ВС​

Для начала, давайте разберемся с тем, что такое трапеция. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие - нет.

Чтобы решить задачу, нам понадобятся свойства трапеции. Одно из основных свойств трапеции заключается в том, что сумма двух противоположных сторон равна сумме двух других.

В этой задаче, мы знаем длины диагоналей BD и АС, а также длины отрезков ВО, СО, DO и АО. Мы хотим найти длину отрезка ВС.

Для начала, мы можем воспользоваться свойством трапеции и записать уравнение:

ВО + СО = DO + АО

Теперь подставим известные значения:

4 + 5 = 12 + 15

9 = 27

Но это уравнение неверное, поэтому что-то делаем не так.

Обратимся к другому свойству трапеции: диагонали трапеции делятся точкой их пересечения на две равные части. То есть, отрезок ОВ равен отрезку ОС, и отрезок ОА равен отрезку OD.

Мы можем использовать это свойство для нахождения величин ВО и АО. Поскольку ОВ равно ОС, мы можем записать:

ВО = СО

4 = 5

Также, ОА равно ОD, поэтому мы можем записать:

АО = OD

15 = 12

Теперь мы можем подставить эти значения в наше уравнение и решить его:

ВО + СО = DO + АО

4 + 5 = 12 + 15

9 = 27

У нас снова получилось неверное уравнение. Значит, что-то не так.

Если мы обратим внимание на рисунок, то заметим, что отрезок ВО и отрезок АО являются продолжениями оснований трапеции. Поэтому, сумма отрезков АО и ОВ должна быть равна длине основания АС. И сумма отрезков ОВ и СО должна быть равна длине основания BD.

Теперь мы можем записать уравнение:

АО + ВО = АС

15 + 4 = АС

19 = АС

Аналогично,

ВО + СО = BD

4 + 5 = BD

9 = BD

Теперь, у нас есть длины оснований трапеции: АС = 19 и BD = 9. Мы хотим найти длину отрезка ВС.

Обратим внимание на то, что отрезок ВС является рзностью длин основания АС и BD:

ВС = АС - BD

ВС = 19 - 9

ВС = 10

Таким образом, длина отрезка ВС равна 10.

Ответ: ВС = 10.