В трапеции ABCD с основаниями ВС и AD углы ABD и ACD прямые. а) Докажите, что АВ = CD.
б) Найдите AD, если AB = 2, BC = 7.
Другие вопросы по теме Геометрия
Популярные вопросы
- Яка маса кошика яблук, якщо на нього діє сила тяжіння 500 h...
2 - Выполнить действия 1) (2,6+3,7)*5 2) (18,07-6,03)*8 3) (24,95+17,8)*9...
1 - Вставить пропущенные слова: i make my bed. i never have for my breakfast/...
2 - Амного ль рассветов ты встретил в лесу разобрать по частям речи определить...
3 - Здвох мист,видстань миж якими 540км,виихали одночасно назустрич один...
2 - Деление с остатком. сравни. реши 72: 2 72: 3 42: 2 42: 3 52: 2 52: 3...
3 - Перевести на казахский только правильно мне нужно . я хожу каждый день...
3 - Перевод с на countries and people...
1 - Решите пример по действиям 60.997+(6012+6228): 30=? 1) в скобках 2) деление...
3 - Втрёх вагонах поезда едут 100 пассажиров. в первом и во втором 66 пассажиров,а...
2
8 ед.
Объяснение:
Дано: ABCD - трапеция.
∠ABD = ∠ACD = 90°
AB = 2, BC = 7.
Доказать: АВ = CD;
Найти: АD.
Доказательство:
Рассмотрим ΔABD и ΔACD - прямоугольные.
Проведем медианы ВО и СО соответственно.
Так как AD - общая для данных треугольников, то медианы пересекут AD в точке О.
Медиана, проведенная из прямого угла прямоугольного треугольника к гипотенузе, равна половине гипотенузы.
⇒ АО = OD = OC = OB.
⇒ точки A, B, C, D будут лежать на одной окружности, то есть вокруг данной трапеции можно описать окружность.
Если вокруг трапеции можно описать окружность, то трапеция равнобедренная.
⇒ АВ = CD
Проведем высоту ВН.
В равнобедренной трапеции высота, опущенная из вершины тупого угла на основание, делит это основание на отрезки, меньшее из которых равно полуразности оснований.
⇒ АН = (АD-ВС):2 = (AD-7):2
Пусть АН = х, тогда х = (AD-7):2
или AD=2x+7
Рассмотрим ΔАВН и ΔABD - прямоугольные.
∠А - общий.
⇒ ΔАВН ~ ΔABD (по двум углам)
Составим пропорцию:
x₂ - не подходит
⇒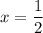
AD = 2x+7 = 8(ед)