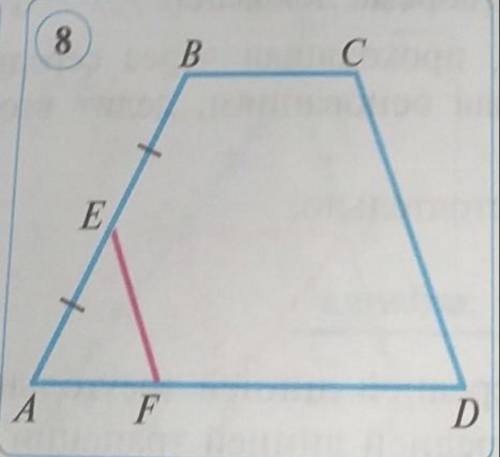
В трапеции ABCD отрезок EF параллелен стороне CD а точка E середина ab докажите что EF 0.5CD
Другие вопросы по теме Геометрия
Популярные вопросы
- 11. Укажіть речення, у якому вжито модальну частку. (Кількість балів 1.00)Б...
3 - Определить% -ный содержание NiCl2 * 6 H2O в реактиве, если навеску 2,1234...
2 - Поміркуйте і дайте відповідь, у сітківці сови є самі палочки, у сітківці...
2 - в сосуд с водой погружен куб со стороной 5 см расстояние от верхней грани...
2 - Малюнок панно моя україна...
1 - Визначте мовні засоби зв язку речень у тексті 1) Восени відлітають птахи....
3 - Вычислить площади фигур, ограниченных линиями, заданными явно, параметрически...
3 - Багатоклітинне вегетативне тіло гриба - це...
3 - Литр бензина стоит 1,328€. Сколько будет стоить литр бензина, если его...
1 - Простой тест 1. Mother doesn t have much free time. Neither .. a) do I,...
2
В данной задаче нам нужно доказать, что отрезок EF равен половине отрезка CD.
Для начала, давайте разберемся с тем, что означают термины "трапеция", "параллельность сторон" и "середина отрезка".
Трапеция - это четырехугольник, у которого две противоположные стороны параллельны. В нашем случае трапеция обозначена буквами ABCD.
Параллельность сторон - это свойство фигур, когда их стороны идут одна рядом с другой и никогда не пересекаются. В данной задаче сказано, что отрезок EF параллелен стороне CD.
Середина отрезка - это точка, которая деляет отрезок на две равные части. В данной задаче сказано, что точка E - середина отрезка AB.
Теперь перейдем к доказательству. Нам нужно показать, что длина отрезка EF равна половине длины отрезка CD.
Для этого рассмотрим треугольники ABE и CDE.
1. Так как точка E является серединой отрезка AB, то отрезок AE равен отрезку BE. (Обоснование: свойство точки, являющейся серединой отрезка.)
2. Также, так как точка E является серединой отрезка AB, то отрезок EC равен отрезку ED. (Обоснование: свойство точки, являющейся серединой отрезка.)
3. Так как отрезок EF параллелен стороне CD, то угол EFC равен углу CDE. (Обоснование: параллельные стороны создают равные углы с пересекающими их прямыми.)
4. Теперь рассмотрим треугольники EFC и CDE. У них две пары равных сторон (отрезок EF равен отрезку CD, и отрезок EC равен отрезку ED), и у них равные углы (угол EFC равен углу CDE). Поэтому эти треугольники равны. (Обоснование: свойство равенства треугольников, когда у них равные стороны и равные углы.)
5. Так как треугольники EFC и CDE равны и отрезок EF равен отрезку CD, то каждая сторона треугольника EFC равна соответствующей стороне треугольника CDE. В частности, сторона EF равна стороне CD. (Обоснование: свойство равенства треугольников, когда у них равные стороны.)
Таким образом, мы доказали, что отрезок EF равен половине отрезка CD. Ответ на задачу: EF = 0.5CD.