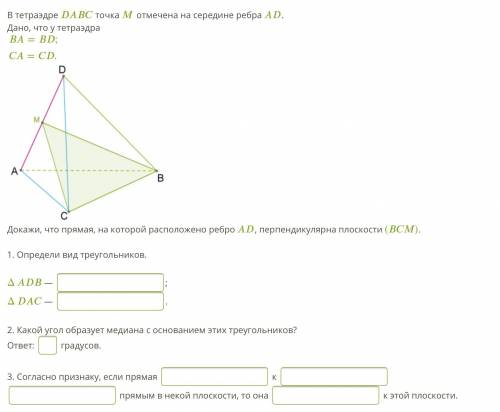
В тетраэдре точка отмечена на середине ребра . Дано, что у тетраэдра
=;=.

Докажи, что прямая, на которой расположено ребро , перпендикулярна плоскости ().

1. Определи вид треугольников.

Δ — ;
Δ — .

2. Какой угол образует медиана с основанием этих треугольников?
ответ: градусов.

3. Согласно признаку, если прямая к прямым в некой плоскости, то она к этой плоскости.

Добрый день! Давайте рассмотрим данный вопрос по шагам для лучшего понимания.

1. Определим вид треугольников.
В данном случае у нас имеются два треугольника ΔABE и ΔBCD, где точка E - середина ребра AD, а точка C - вершина тетраэдра. Треугольник ΔABE является равнобедренным, так как AE является медианой и, следовательно, разделяет боковые стороны AB и BE пополам. Аналогично, треугольник ΔBCD также является равнобедренным, так как CD является медианой и разделяет боковые стороны BC и BD пополам.

2. Рассчитаем угол, образованный медианой.
Мы знаем, что в равнобедренном треугольнике медиана, проведенная из вершины, делит основание на две равные части. Таким образом, медиана AE будет образовывать угол в 60 градусов с основанием треугольника ΔABE и медиана CD будет образовывать угол в 60 градусов с основанием треугольника ΔBCD.

3. Докажем, что прямая, на которой расположено ребро AC, перпендикулярна плоскости ΔABE.
Для этого воспользуемся свойством: если прямая перпендикулярна к прямым, лежащим в плоскости, то она перпендикулярна и к этой плоскости.
Поскольку ребро AC лежит в плоскости ΔABE, и прямая, на которой оно расположено (ось медианы AE), образует угол в 60 градусов с основанием треугольника ΔABE, то эта прямая и плоскость ΔABE будут перпендикулярны.

Таким образом, мы доказали, что прямая, на которой расположено ребро AC, перпендикулярна плоскости ΔABE.