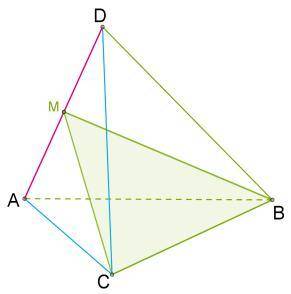
В тетраэдре DABC точка M делит пополам ребро AD.
Известно, что в этом тетраэдре
BA=BD;CA=CD.
На рисунке
Докажи, что прямая, на которой находится ребро AD, перпендикулярна плоскости (BCM).

1. Определи вид треугольников.

ΔADB —
;
ΔDAC —
.

2. Какой угол образует медиана с основанием этих треугольников?
ответ:
градусов.( )

3. Согласно признаку, если прямая
к ( )

прямым в некой плоскости, то она ( )
к этой плоскости.

В тетраэдре DABC точка M делит пополам ребро AD.  Известно, что в этом тетраэдре  BA=BD;CA=CD. На рисунке  . Докажи, что прямая, на которой находится ребро AD, перпендикулярна плоскости (BCM).

Объяснение:

1. В тетраэдре все  боковые ребра , проведенные из вершины тетраэдра , равны. По условию BA=BD;CA=CD ,значит ΔADB –равносторонний,  ΔDAC –равносторонний.

2. По свойству медианы равнобедренного треугольника , она является высотой, значит ВМ⊥ АD и СМ ⊥AD .

Поэтому  угол , который образует медиана с основаниями  этих треугольников равен 90°

3. Согласно признаку перпендикулярности прямой и плоскости , если прямая перпендикулярна к двум пересекающимся прямым МС и МВ , лежащим в плоскости ВСМ, то она перпендикулярна к этой плоскости (ВСМ).